What’s the Winkel Tripel BOPC?
The name »Winkel Tripel BOPC« was made up for this website.
However, I didn’t come up with the idea for this variant and quite possibly it has been used before.
Learn more about this matter (and about the abbreviation BOPC) here.
Oswald Winkel designed the Winkel Tripel in 1921 by calculating the arithmetic mean of the Equirectangular and the Aitoff projections. On the Equirectangular you can set the standard parallels, and Winkel chose approx. 50°28´ – that’s arccos(2/π) to the mathematicians [1] – before mixing it with the Aitoff.
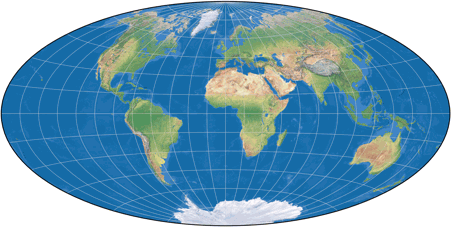
The Aitoff projection…
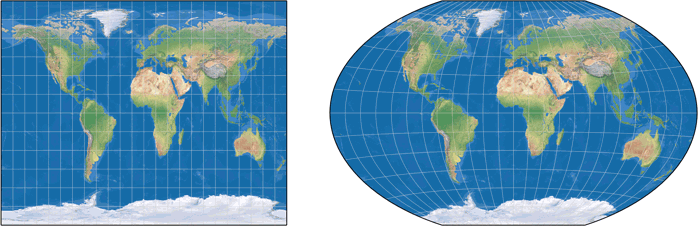
… arithmetically averaged with Equirectangular, standard parallels at approx 50°28´,
results in the original Winkel Tripel.
About 1955, John Bartholomew designed a Winkel Tripel variant for the Times Atlas, in which he chose 40° as
standard parallels for the Equirectangular portion of the projection. The resulting projection is wider
than the original and many people will argue (and I agree with them) that it shows a better distribution
of distortions. By the way, Karlheinz Wagner pointed out already in 1949, that this value
»seems to be the most appropriate for a world map« and presented a corresponding figure.
[2]
Here in this website, this variant is filed under »Winkel Tripel Bartholomew«.
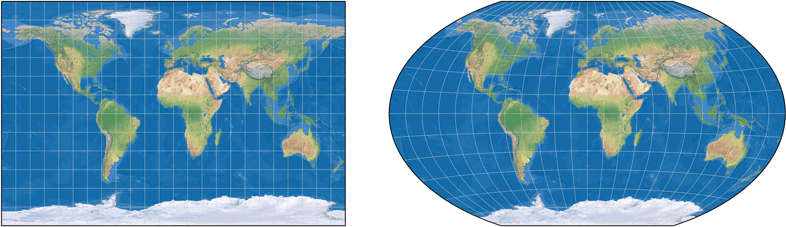
Setting standard parallels to 40° on the Equirectangular portion will give you Winkel Tripel Bartholomew.
However, in a forum thread on mapthematics.com
I found the assertion that there is a third variant of Winkel Tripel: The Oxford Atlas version with 0° as
standard parallel in the Equirectangular portion, which of course is the plate carrée projection.
Now, the application Geocart offers the option to blend two projections. And so, I blended the Aitoff and
plate carrée projections and voilà, I had the Oxford Atlas version.
[3]
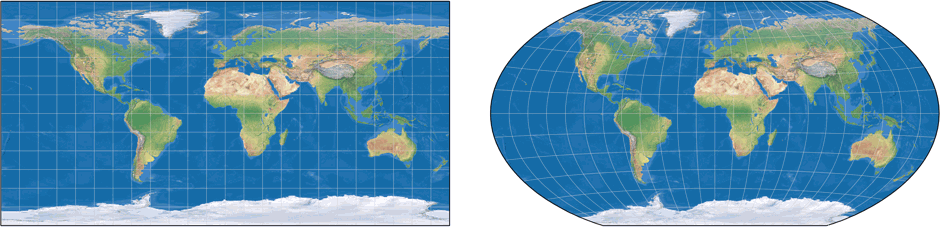
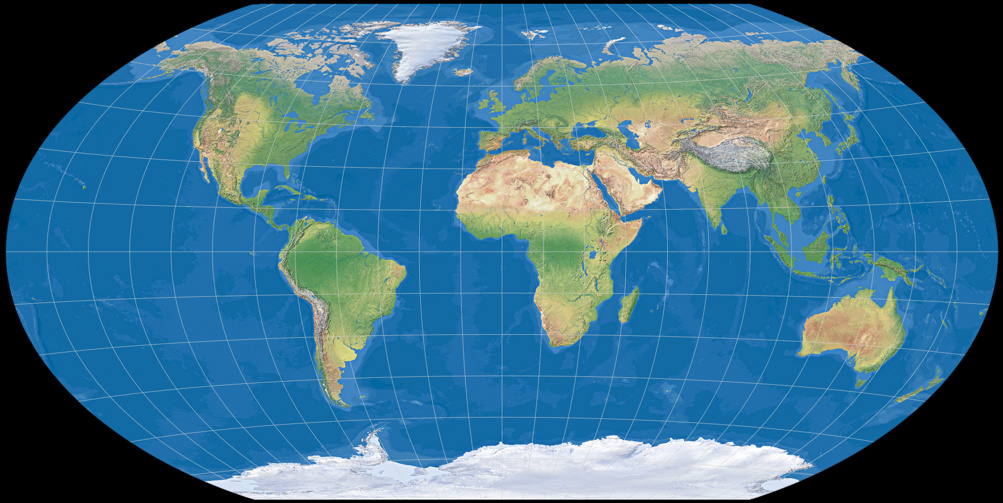
Throwing Plate carrée into the mix – a new Winkel Tripel version!
My first thought was to put it on the website using the name Winkel Tripel Oxford Atlas, but…
besides the aforementioned forum entry, I couldn’t find a single evidence on the web that there ever was an Oxford Atlas
using this map.
Of course, things like this happen. You probably wouldn’t find out which projection is used for the world map in my
1997 Meyers Atlas, too. So this doesn’t mean that the Oxford Atlas never used a Winkel Tripel having the reference parallels at 0°.
But as long as I couldn’t find any proof, I was reluctant to use this name. Moreover, the
Gall-Bomford projection is sometimes referred to as »Oxford Atlas projection«
[3]
so it might be a better idea to choose a different name in order to avoid confusion.
So for now, I just called it Winkel Tripel based on plate carrée – or, abbreviated,
BOPC.
I might change the name if I find ever find out that there already is an established name for this variant.
Winkel Tripel BOPC
Footnotes
-
↑
arccos(2/π) is not exactly 50°28´, but – in case I didn’t miscalculate this –
50,45977625219° or 50°27´35.1945″. But you can safely disregard this: On a printed map, the difference is probably
less than the warpage of the paper the map is printed on.
And in an digital image having a width of about 12,000 pixels the maximum difference is two pixels. (And yes, I was crazy enough to try…) -
↑
Wagner, Karlheinz:
Kartographische Netzentwürfe.
Leipzig 1949, page 225 - ↑ I don’t know what Geocart is exactly doing when you blend two projections. Is this even related to the arithmetic mean after all? However, when I choose the Winkel Tripel Bartholomew directly from Geocart’s menue on one hand, and blend the Equirectangular projection (standard parallels at 40°) with Aitoff on the other, the results are identical. So it’s safe to say that my blended Winkel Tripel BOPC, for all intents and purposes, matches the actual arithmetic mean.
- ↑ see libproj4: A Comprehensive Library of Cartographic Projection Functions, Gerald I. Evenden, November 22, 2008, page 78; pulled at 2016-11-15.
Comments
2 comments
Piotr Grochowski
Geocart blending is confirmed to be averaging for 0.5, and linear weighting for other priorities. https://www.mapthematics.com/f…
Peter Denner
Do you think this is evidence that there really was an Oxford Atlas using this variant of the Winkel tripel? Or just evidence that the people at GISS read your blog (or the mapthematics forum)?
Tobias Jung
jayden
Jonas
And keeping the correct 2:1 parallel/meridian ratio, bearable inflation and distortion, and no vertical distortion in the middle of the map, Wagner VI is my favorite of them all. (I hate when Africa and South America are vertically elongated!)
By the way, this site is amazing. Thank you!
Tobias Jung
Wether straight parallels are an advantage or not, is of course open to debate…
And thank you for your kind words! :-)