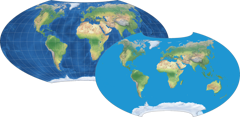
Web site archive: Approximations
There are no approximations anymore on map-projections.net.
The text below was only kept in case anyone’s interested in what this was all about.
Most projection image on this website were generated using applications that work
with the creator’s orginal formula.
In some cases, that wasn’t possible and I couldn’t find an appropriate image on the web either.
So I used Flex Projector to reproduce the projection in question.
I succeeded to some degree, but none of my recreations is absolutely accurate. That’s why they’re called
approximations.
Here, I’m going to list these approximations, tell you how I created them and how close they are to the original projection.
See below if you’re interested in improving the approximations!
Eckert II
All Eckert II images are approximations which were generated in Flex Projector from the Eckert I
by changing the Distance and Length values of the parallels.
It’s a very close approximation, but Flex Projector is showing an areal distortion value of 0.01,
whereas an equal-area projection of course should have 0.00.
Moreover, although the meridians look like perfectly straight lines, they actually aren’t.
For an image that is actually based on Eckert’s original formula, please refer to
commons.wikimedia.org/wiki/File:Eckert_II_projection_SW.JPG.

Eckert II, generated by the original formula (left) and approximated (right)
Hufnagel 7, 9 und 10
The physical maps of the Hufnagel projections are images by Daan Strebe, which are based on the original formula. The other projection images (silhouette maps and Tissot indicatrix) were generated from approximations build in Flex Projector.
The Hufnagel 7 images are based on Wagner VII. I removed the bending of the parallels, changed their position and length
and edited the distribution of merdians.
Having an areal distotion value of 0.03 (instead of 0.00), this approximation is deviating from the original more than
the other ones, but still, it’s close enough for the matters of comparison – after all, scaling the images down to a
width of about 1000 pixels (as I do for the presentation here) does hide a few of the shortcomings…

Hufnagel 7, generated by the original formula and the approximated silhouette map
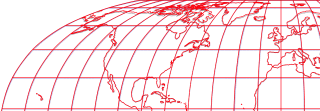
Hufnagel 7 approximation graticule superimposed over the original
Hufnagel 9 is very similar to Eckert IV – so of course, I used Eckert’s projection to start
approximating the Hufnagel 9. I just had to change the position and length of the parallels a bit –
the areal distortion value is correctly at 0.00 – but limited to continental areas only, it’s up to 0.01,
so there still have to be minor deviations.
I only whish I knew how to erase them…

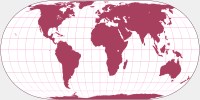
Hufnagel 9, generated by the original formula and the approximated silhouette map
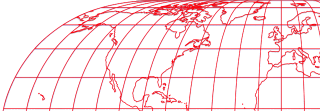
Hufnagel 9 approximation graticule superimposed over the original
Hufnagel 10 images are based on Eckert IV, too, but I had to apply more changes than on the Hufnagel 9. And so, the deviations from the original are greater: The areal distortion values are at 0.01 (general distortion) and 0.02 (continental areas).
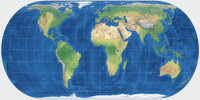
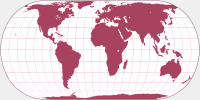
Hufnagel 10, generated by the original formula and the approximated silhouette map
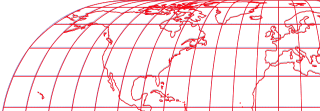
Hufnagel 10 approximation graticule superimposed over the original
Tobler Hyperelliptical Projection
On Tobler’s projection, I was able to generate a very close approximation:
It almost precisely overlays above the graticule in Daniel Strebe’s image (which was generated from the original formula), merely
between 80° North/South and the poles, there are minor deviations. Especially at 85° you see that the meridians bend quite strangely…
Nonetheless I think they are neglectable, at least in the resolution that
is used for the images on this website.
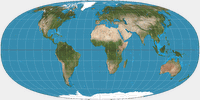
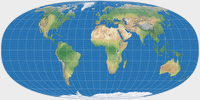
Tobler Hyperelliptical Projection, generated by the original formula (left) and approximated (right)
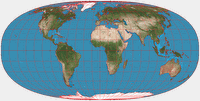
Tobler Hyperelliptical projection, approximation graticule superimposed over the original
Wagner IV
I built the previously mentioned approximations because it was the only way for me to generated images of the according projections.
The Wagner IV approximation, however, was made just because of the fun of it – and because I wanted to see whether the
approach I thought of will lead to appropriate results:
Using an available vector graphic of the Wagner IV graticule, I was able to measure the length of the parallels and their distance
to the equator. Then, I converted these values to values that can be processed by Flex Projector, and copied them to a Flex Projector file
(which originally was an exported file of the Wagner VI projection). I opened the resulting file in Flex Projector –
and indeed I ended up having a close approximation of Wagner IV.
At the center of the projection the approximation’s graticule precisely overlays the graticule of the original, but towards the edges, the approximation increasingly deviates. I guess it’s possible to eliminate the deviations – if you’re willing to put some work into it, which I wasn’t… ;-)
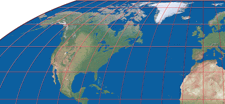
Wagner IV projection, approximation graticule superimposed over the original
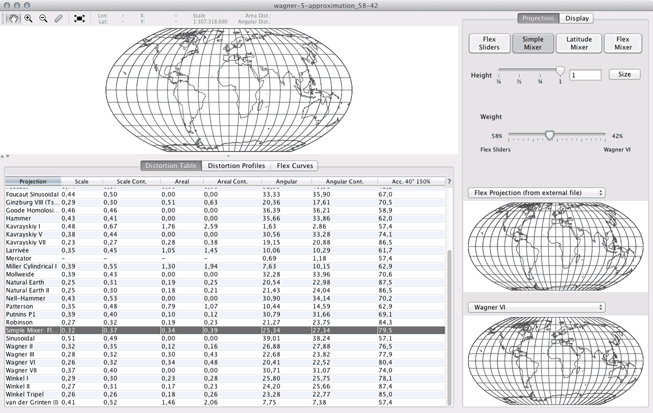
Using this Wagner IV approximation you also can build your own approximation of Wagner V:
- Go to Flex Projector’s Simple Mixer.
- In the first menu, choose Flex Projection (from external file) and select the wagner-4-approximation.txt file.
- In the second menu, choose Wagner VI. (If Wagner VI isn’t listed there, goto Flex Projector's preferences and check the Wagner VI entry.)
- Drag the Weight slider until the Flex Sliders projection has 58% and Wagner VI has 42%.
This will give you an projection that is quite close to Wagner V. You then might switch to the Flex Sliders tab to improve.
Download Approximations
As I’ve said above, none of the approximations is perfect.
So maybe you are interedted in improving them?
Here you go:
-
Install Flex Projector.
The applications runs on Windows, Mac OS X and Linux (requires the Java Virtual Machine version 6 or higher). - Download the reference images given below which were generated by Hufnagel’s formula, so you have something to compare to your result.
- And, of course, download the ZIP archives. Each archive contains two plain text files, a »readme« file and the file to open with Flex Projector.
And in case you do come up with an improved version of any projection, I’d be thankful if you’d drop me a line (see Feedback).
Eckert II
– Reference image
– eckert-2-approximation.zip Flex Projector file
Hufnagel 7
– Reference image
– hufnagel-7-approximation.zip Flex Projector file
Hufnagel 9
– Reference image
– hufnagel-9-approximation.zip Flex Projector file
Hufnagel 10
– Reference image
– hufnagel-10-approximation.zip Flex Projector file
Tobler Hyperelliptical Projection
– Reference image
– tobler-approximation.zip Flex Projector file
Wagner IV
– Reference image
– wagner-4-approximation.zip Flex Projector file