My Projection Collection:
Compare Projections
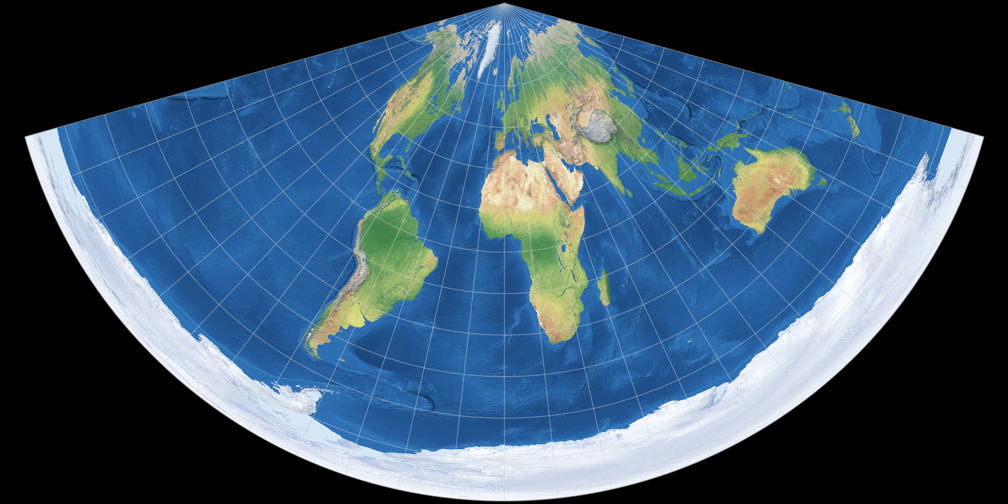
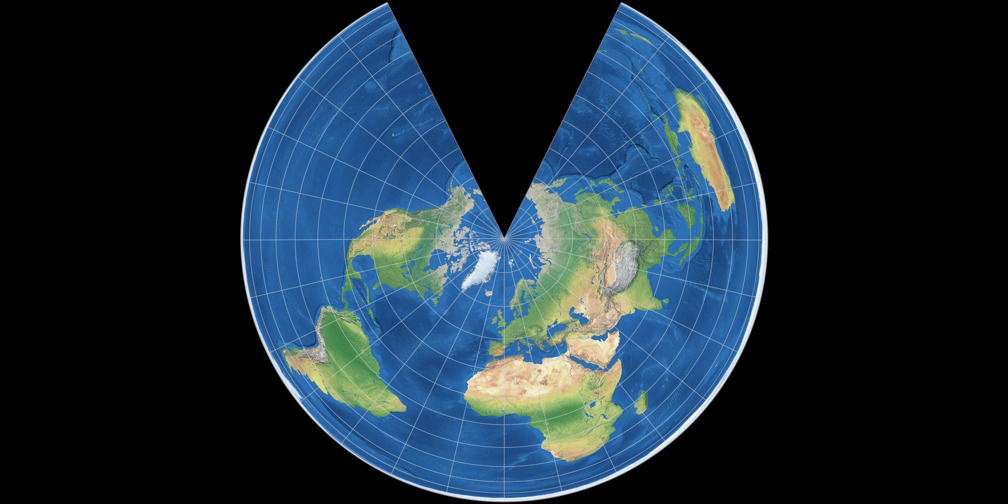
CM Equidistant Conic vs. Lambert Equal-Area Conic
| CM Equidistant Conic | Lambert Equal-Area Conic | |
|---|---|---|
| Creator | Unknown (about AD 100) | Johann Heinrich Lambert (1772) |
| Group | Conic | Conic |
| Property | Equidistant | Equal-area |
| Other Names | — | — |
| Remarks | Standard parallels in the image: 90° North, 30° South. This configuration was set to achieve a result that is comparable to the configuration of Lambert equal-area conic that is shown here on the site. It probably has no practical use, that’s why I chose the name affix CM for compare-maps.net. Equidistant conic projections can be traced back at least to Ptolemy. |
Standard parallel in the image: 10° North. |
| recommended comparisons | Lambert Equal-Area Conic | CM Equidistant Conic |
|
This pairing is among the list of recommended pairings – but why? Well… I just thought it’d be kinda nice to compare an equal-area conic projection to an equidistant one of similar configuration… |
||
1. Comparison: Physical Map – scaled to fit
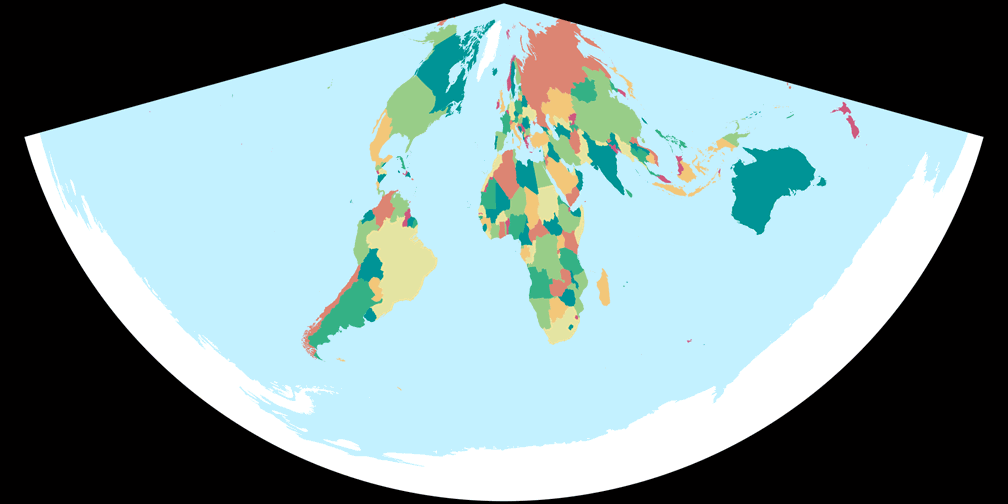
2. Comparison: Political Map – scaled to fit
CM Equidistant Conic
Lambert Equal-Area Conic

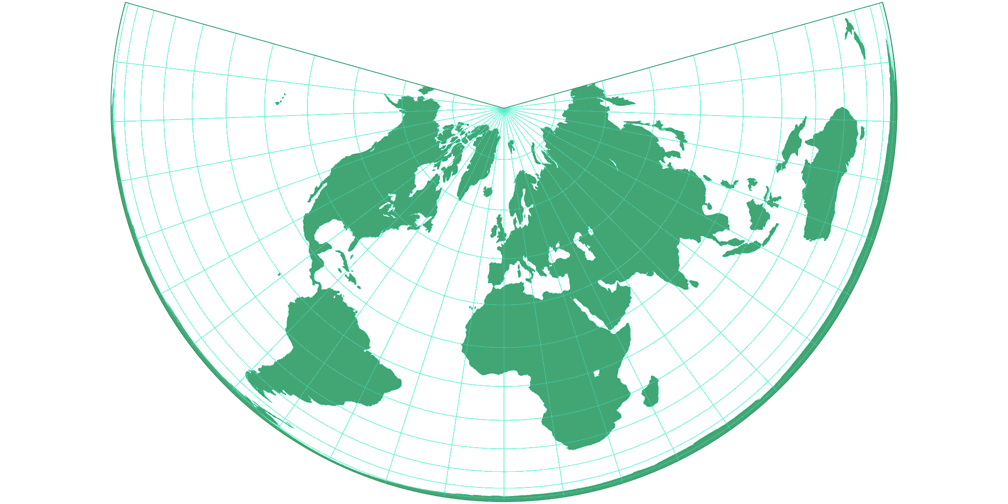
3. Comparison: Silhouette Map – scaled to fit
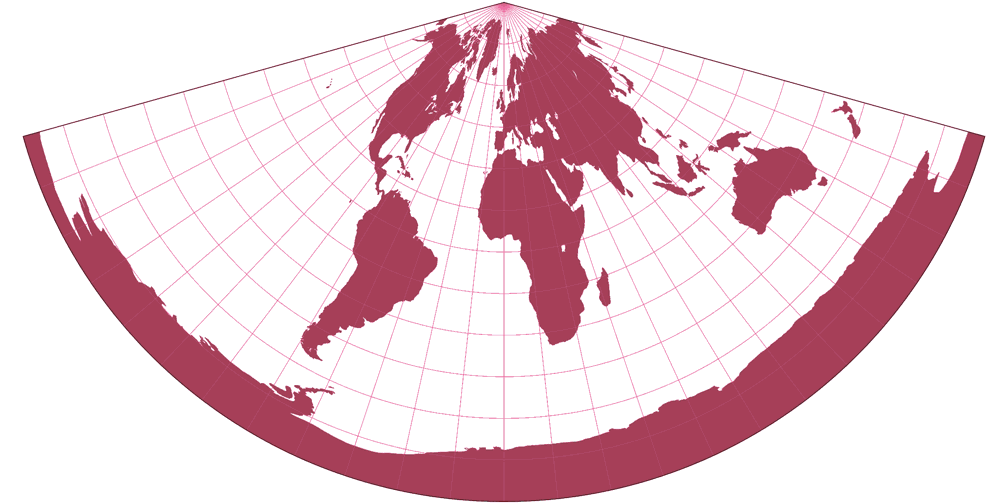
CM Equidistant Conic Silhouette Map c Tobias Jung
Lambert Equal-Area Conic Silhouette Map c Tobias Jung
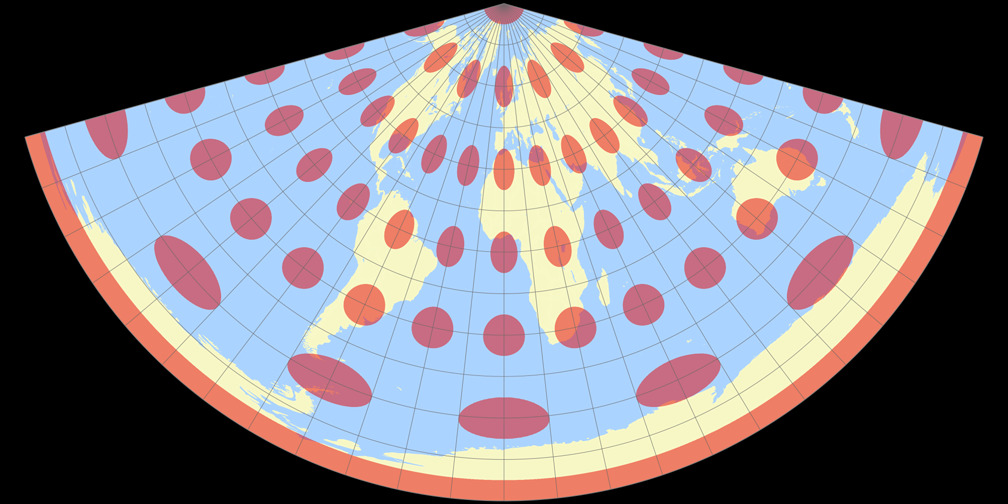
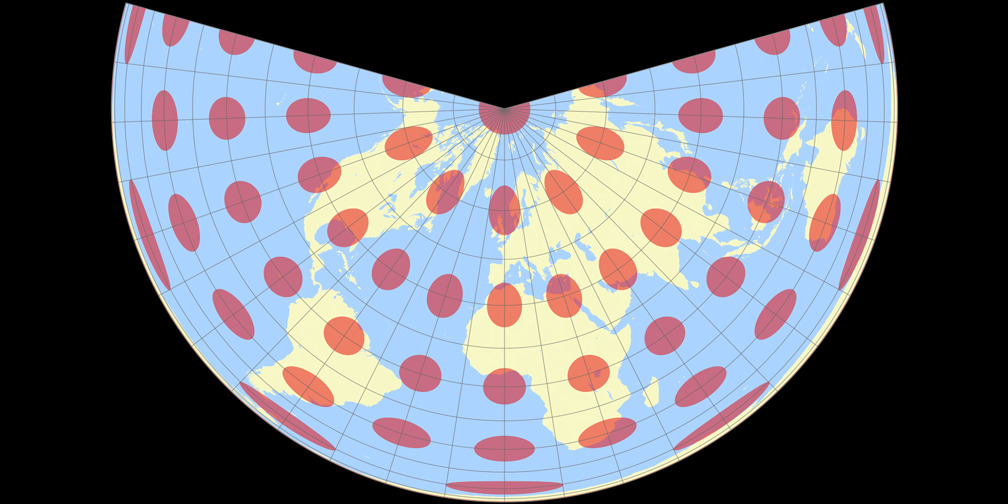
4. Comparison: Tissot Indicatrix, 30° – scaled to fit
CM Equidistant Conic
Lambert Equal-Area Conic
CM Equidistant Conic Tissot Indicatrix c Tobias Jung
Lambert Equal-Area Conic Tissot Indicatrix c Tobias Jung
5. Comparison: Physical Map – scaled to same width
CM Equidistant Conic
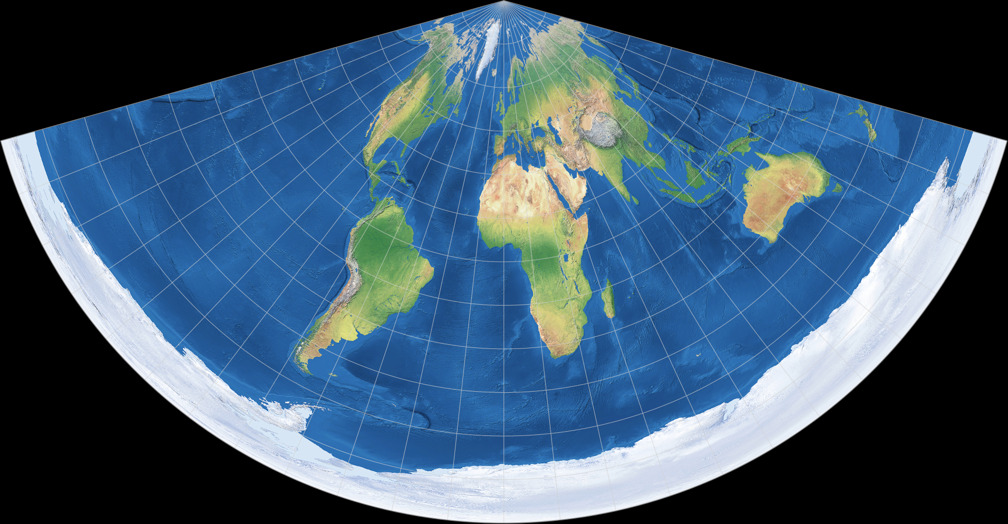
Lambert Equal-Area Conic
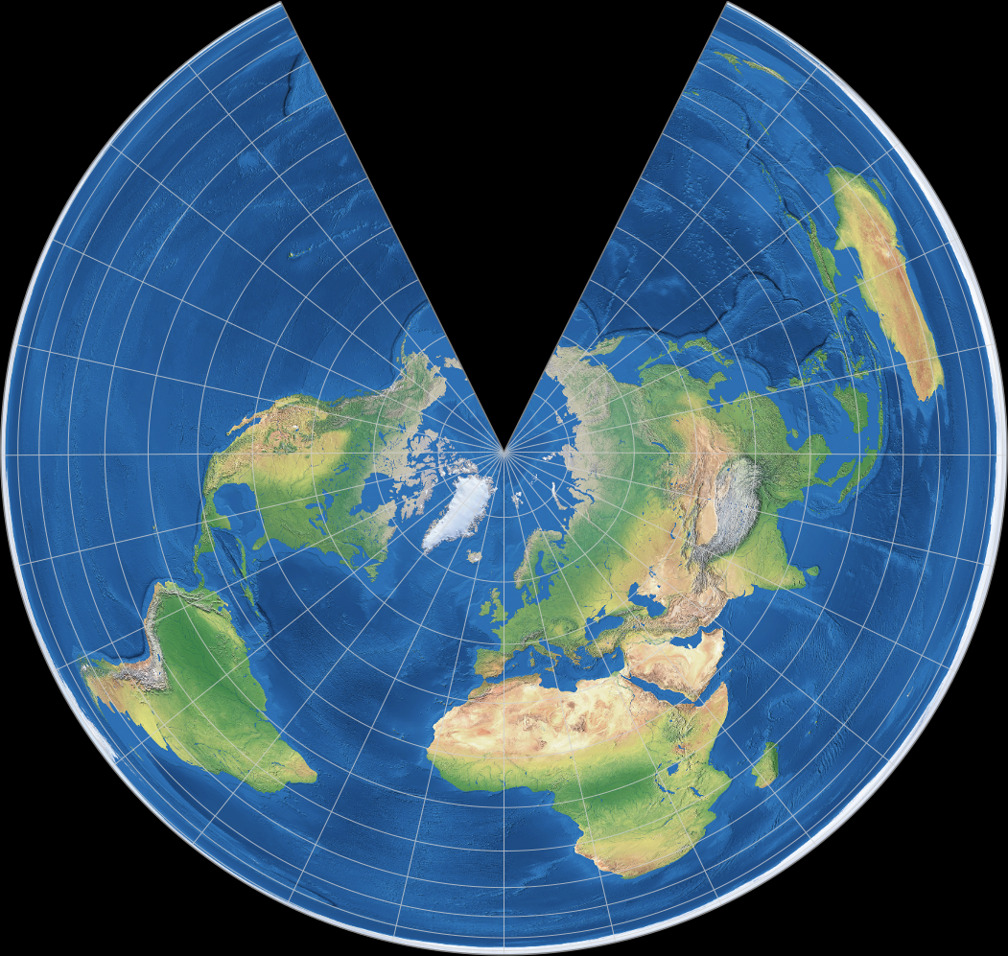
6. Comparison: Political Map – scaled to same width
CM Equidistant Conic

Lambert Equal-Area Conic
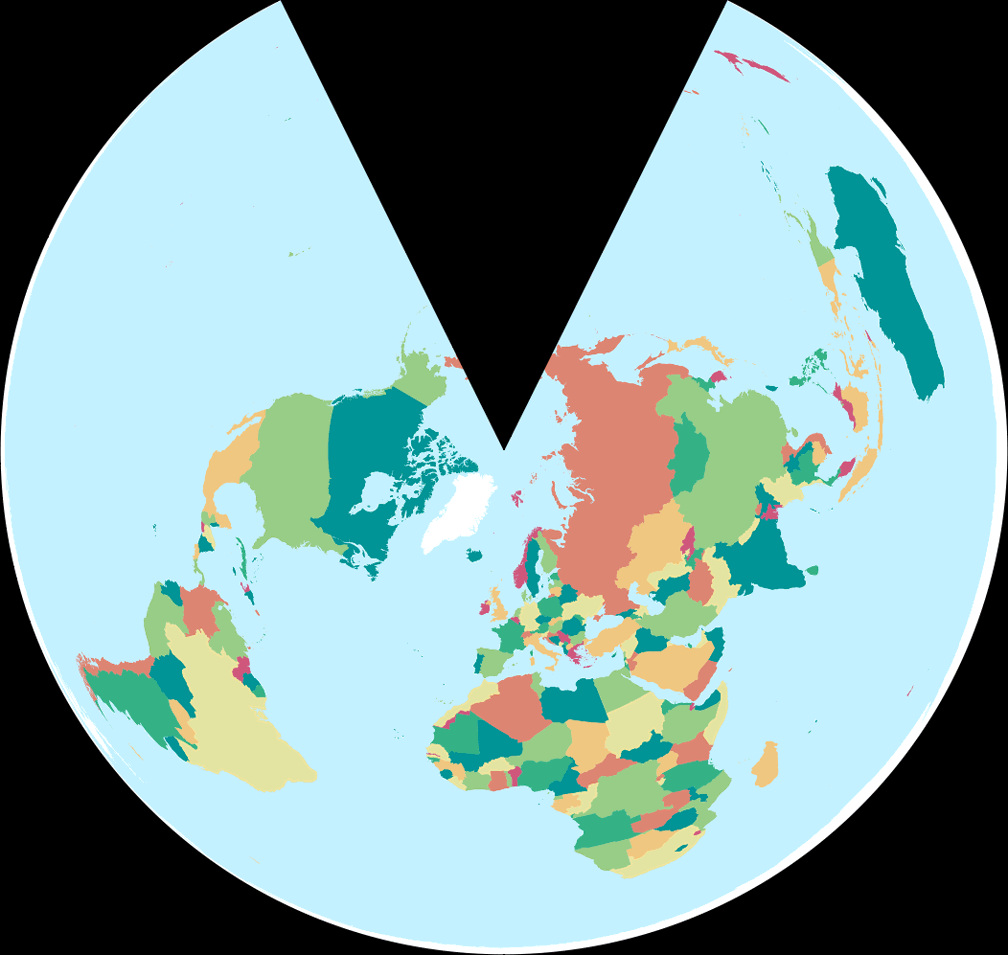
7. Comparison: Silhouette Map – scaled to same width

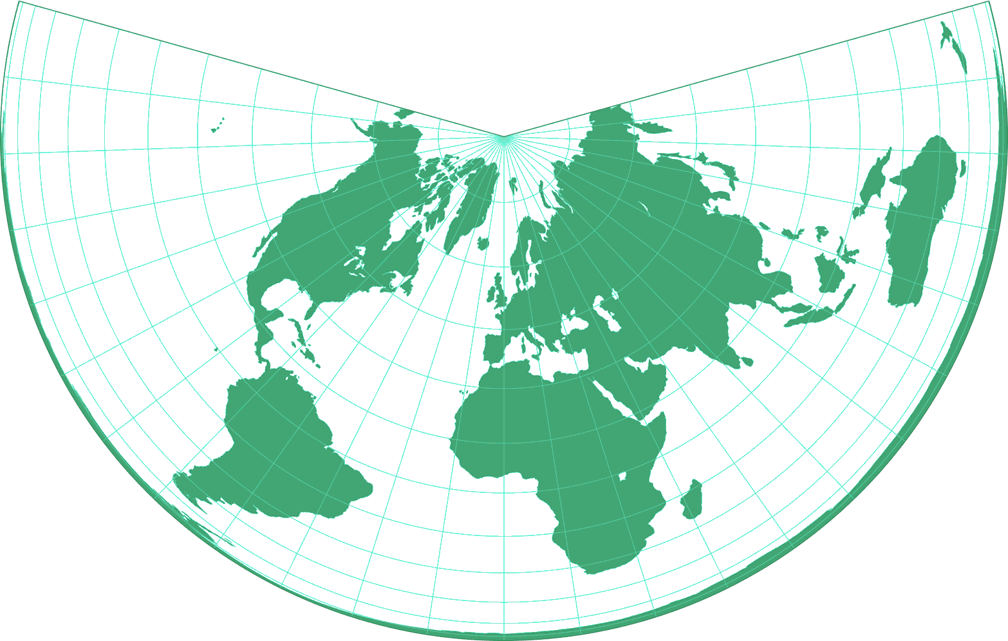
CM Equidistant Conic Silhouette Map c Tobias Jung
Lambert Equal-Area Conic Silhouette Map c Tobias Jung
8. Comparison: Tissot Indicatrix, 30° – scaled to same width
CM Equidistant Conic

Lambert Equal-Area Conic
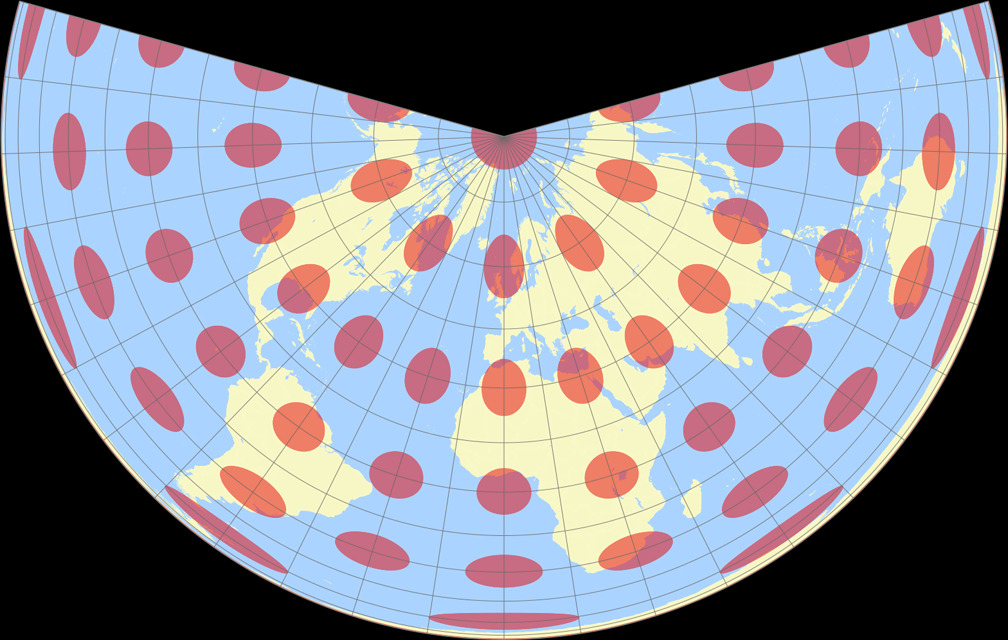
CM Equidistant Conic Tissot Indicatrix c Tobias Jung
Lambert Equal-Area Conic Tissot Indicatrix c Tobias Jung
9. Comparison: Tissot Indicatrix, 15° – scaled to fit
CM Equidistant Conic
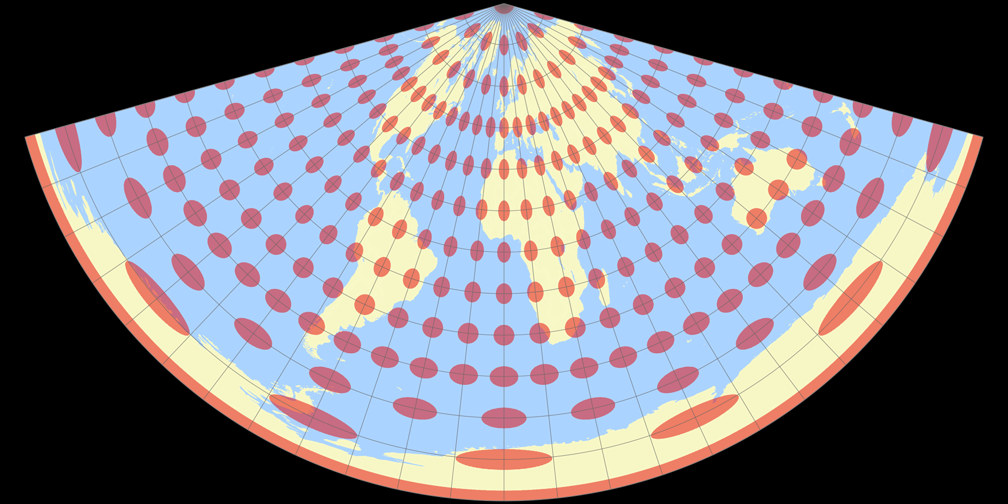
Lambert Equal-Area Conic
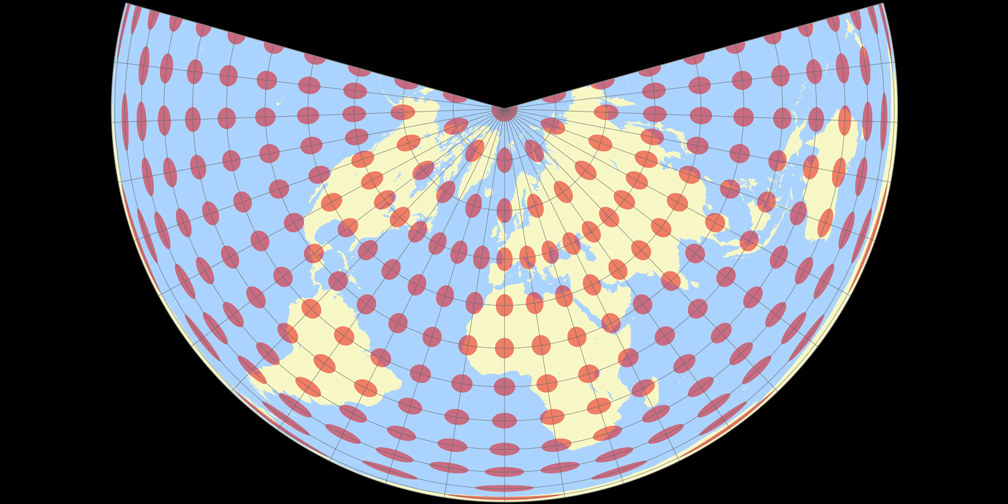
CM Equidistant Conic Tissot Indicatrix c Tobias Jung
Lambert Equal-Area Conic Tissot Indicatrix c Tobias Jung
10. Comparison: Tissot Indicatrix, 15° – scaled to same width
CM Equidistant Conic
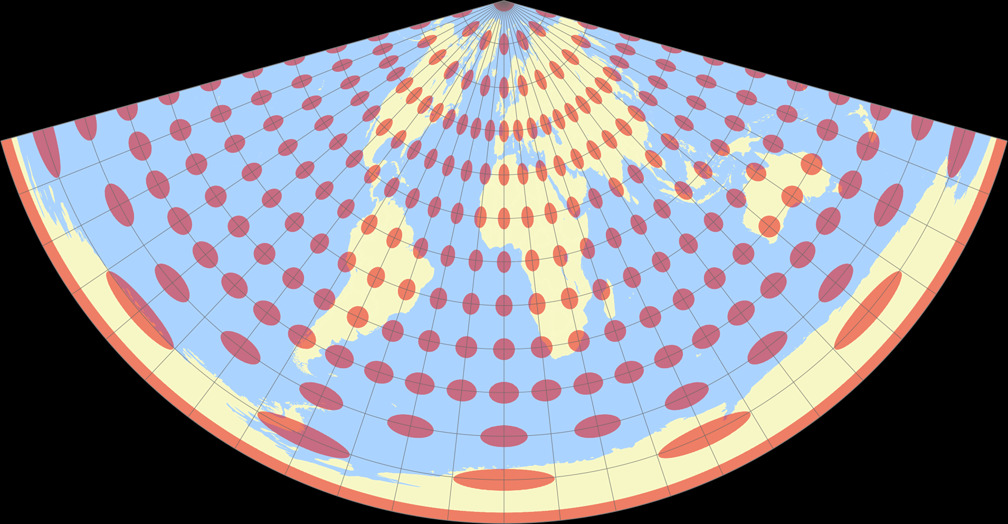
Lambert Equal-Area Conic

CM Equidistant Conic Tissot Indicatrix c Tobias Jung
Lambert Equal-Area Conic Tissot Indicatrix c Tobias Jung