My Projection Collection:
Compare Projections
Breusing Harmonic vs. Nicolosi Globular
| Breusing Harmonic | Nicolosi Globular | |
|---|---|---|
| Creator | A. E. Young (1920) | Abū Rayḥān al-Bīrūnī (1000 approx.) |
| Group | Azimuthal | Miscellaneous |
| Property | Compromise | Compromise |
| Other Names |
|
— |
| Remarks | Modification of Breusing Geometric, Arthur Breusing (1892). | Reinvented by Giovanni Battista Nicolosi, ca. 1660. |
| recommended comparisons | Airy (Hem.) Azimuthal Equidistant (Hem.) Nicolosi Globular |
Azimuthal Equidistant (Hem.) Breusing Harmonic |
|
This pairing is among the list of recommended pairings – but why? These two projections nearly identical, so you might spot the differences in direct comparision only. |
||
Remark: On these two projections, »scaled to fit« and »scaled to same width« will be quite identical!
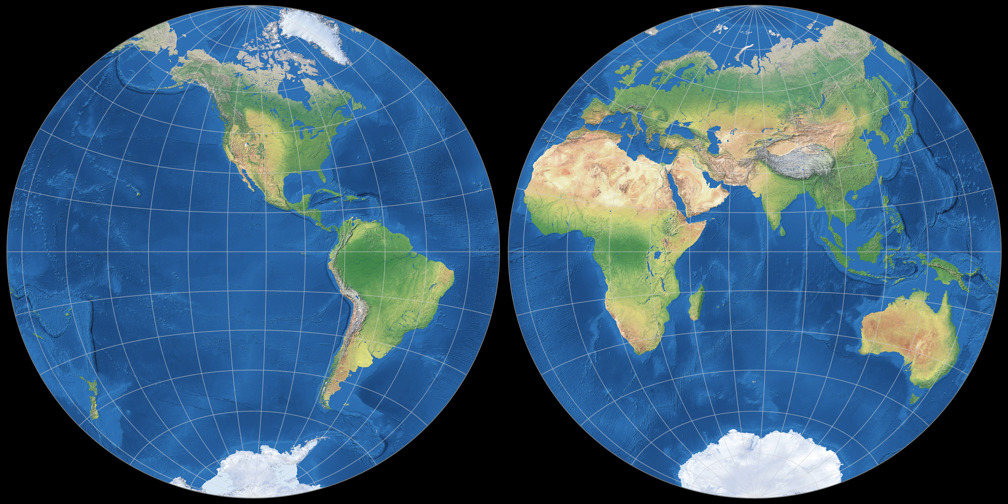
1. Comparison: Physical Map – scaled to fit
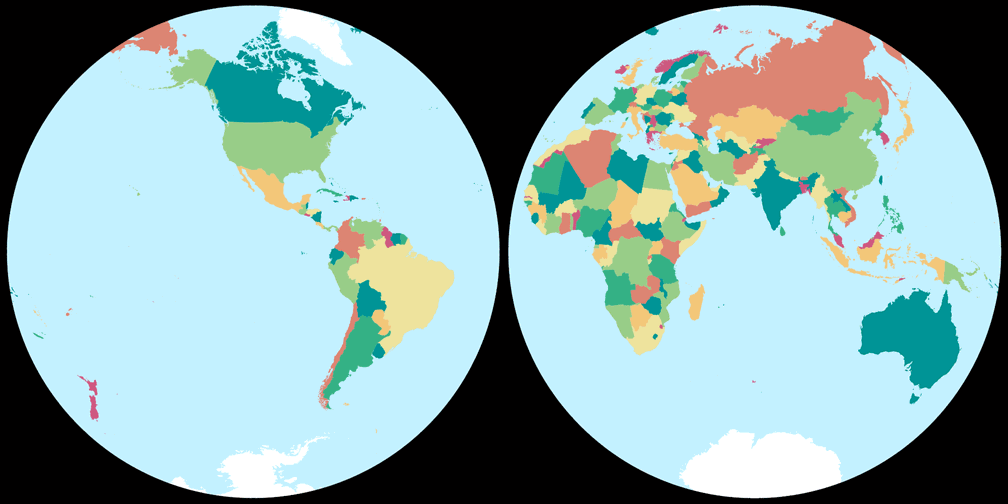
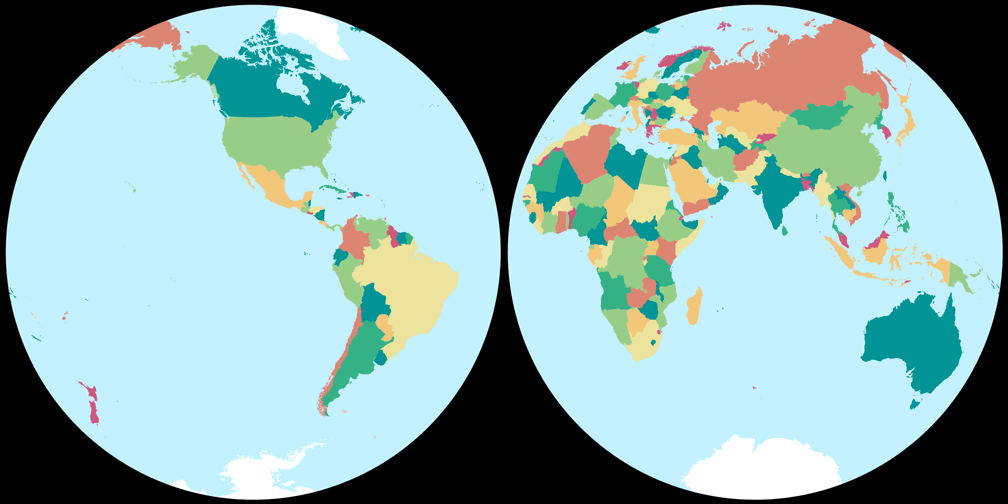
2. Comparison: Political Map – scaled to fit
Breusing Harmonic
Nicolosi Globular
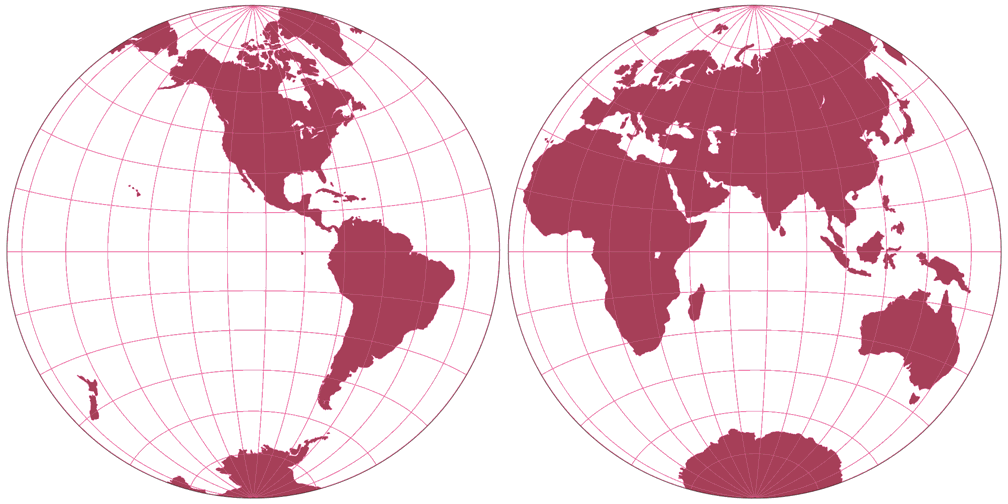
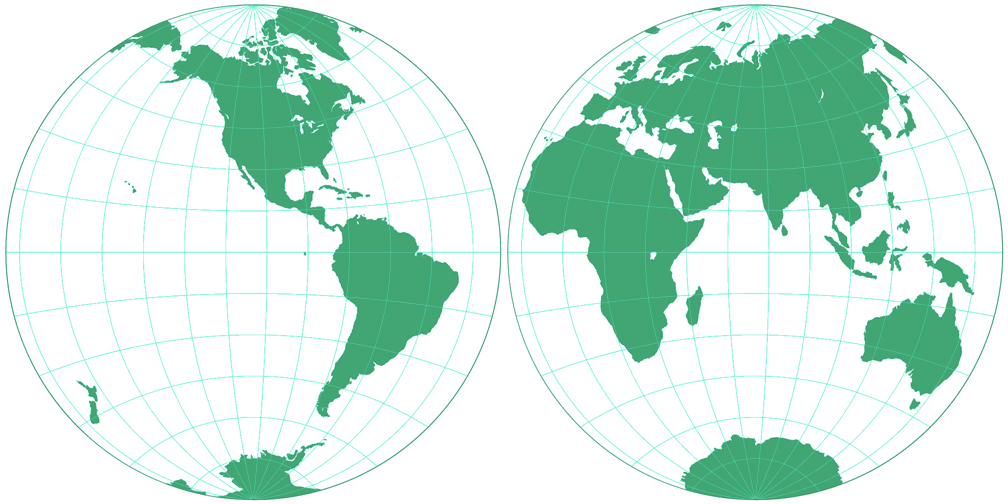
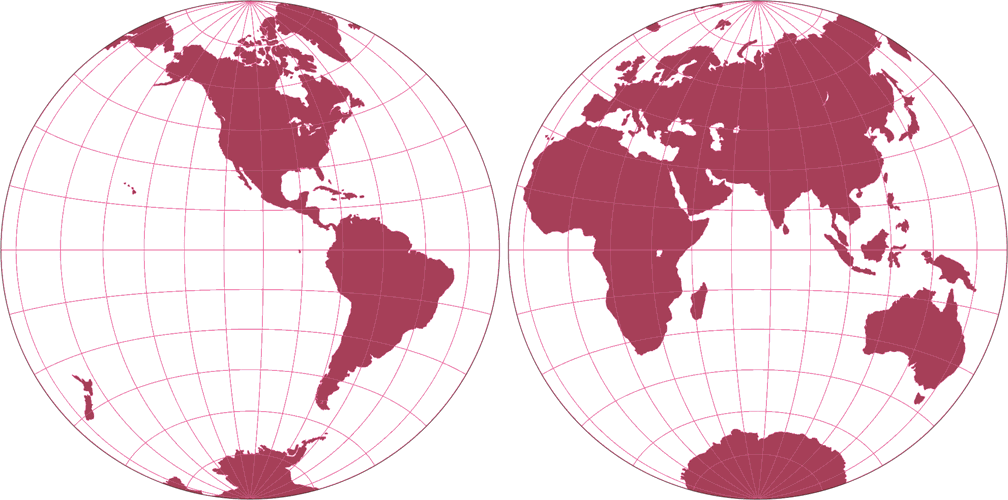
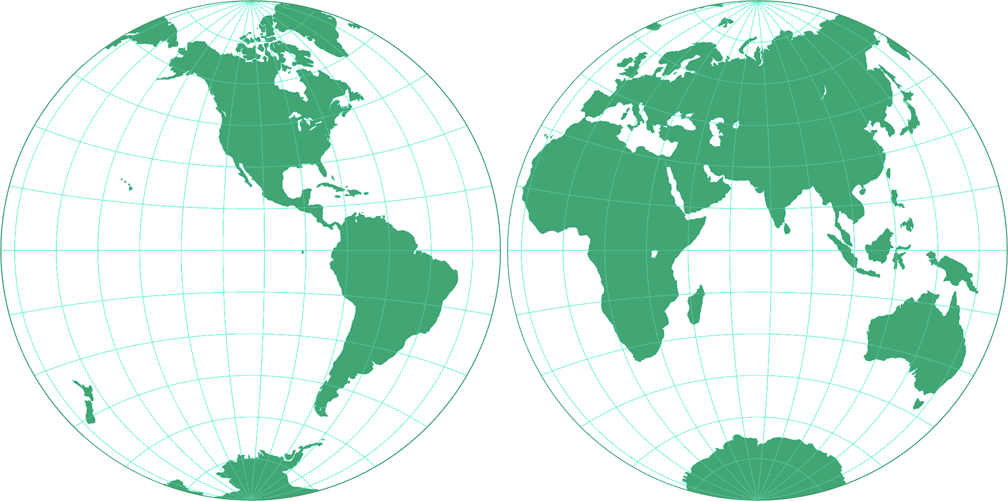
3. Comparison: Silhouette Map – scaled to fit
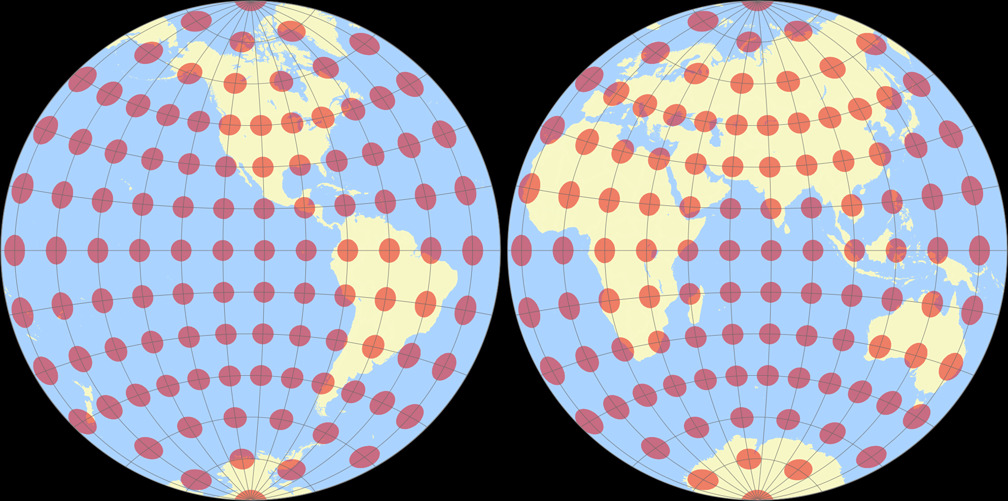
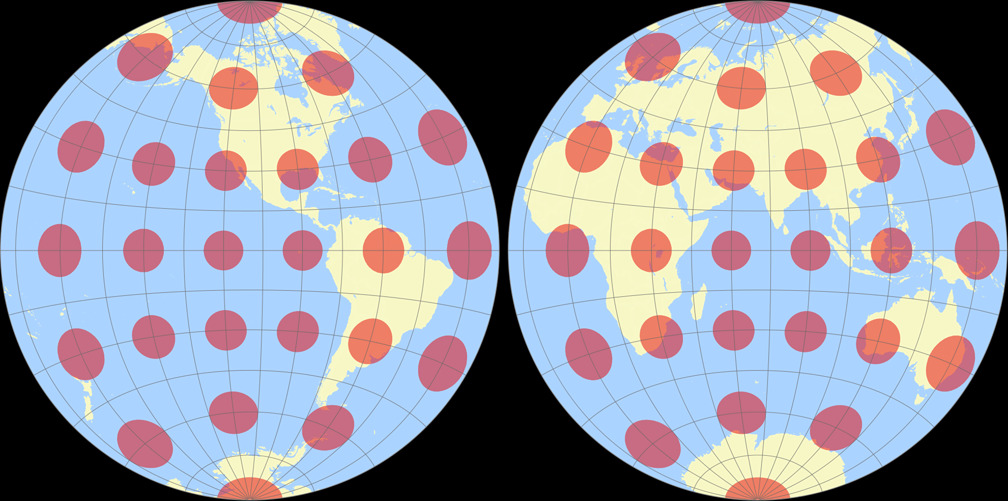
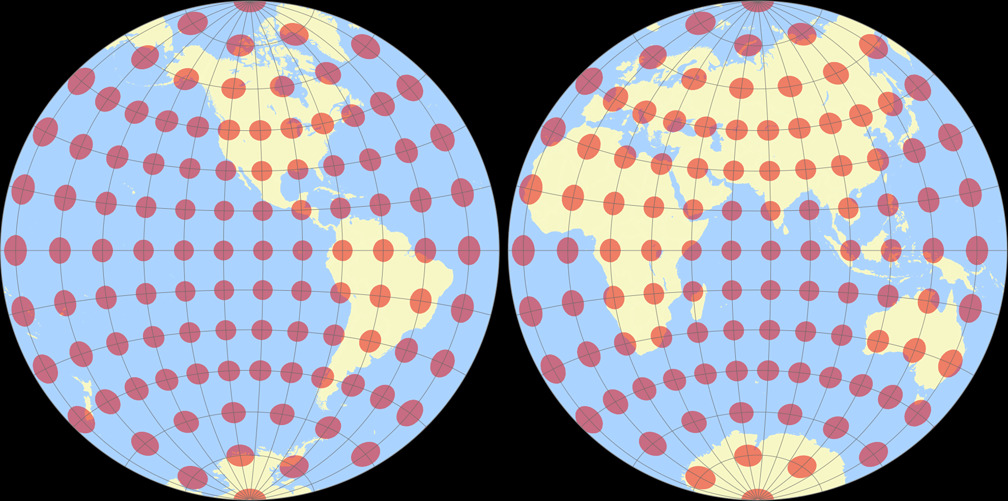
4. Comparison: Tissot Indicatrix, 30° – scaled to fit
Breusing Harmonic
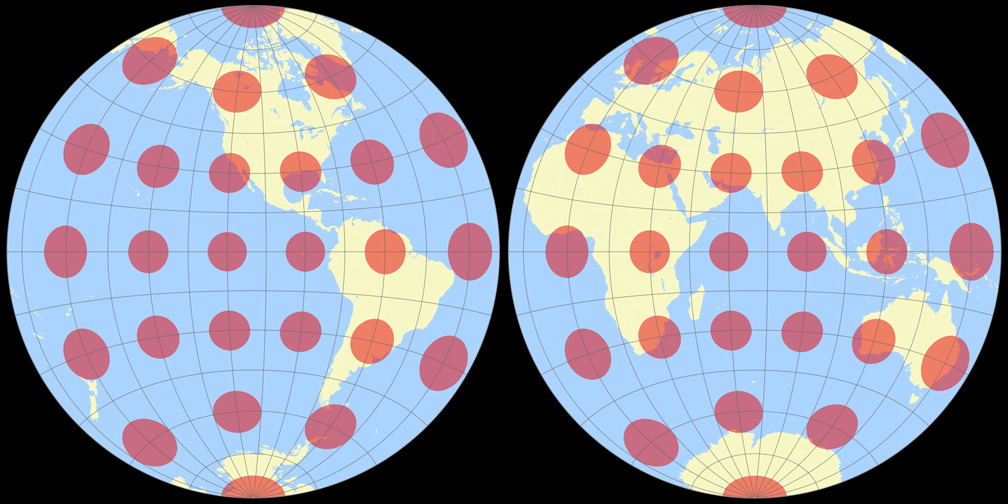
Nicolosi Globular
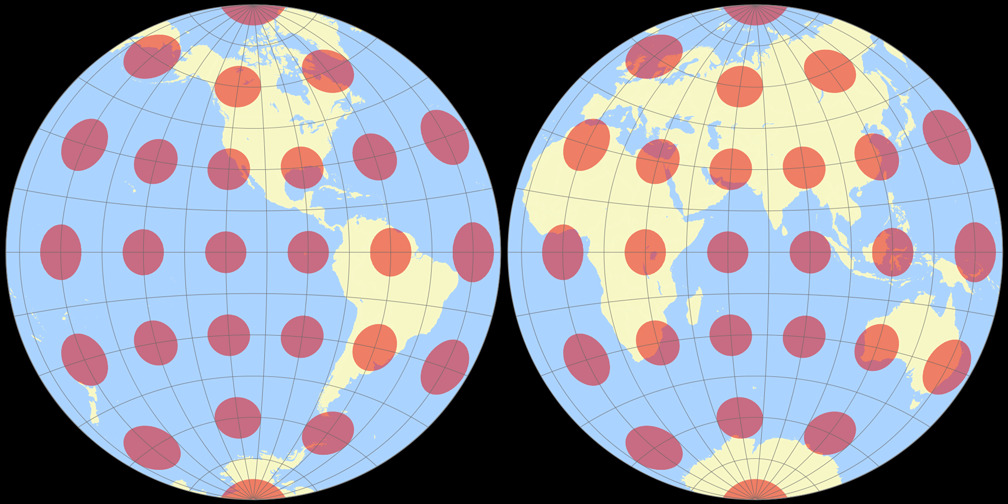
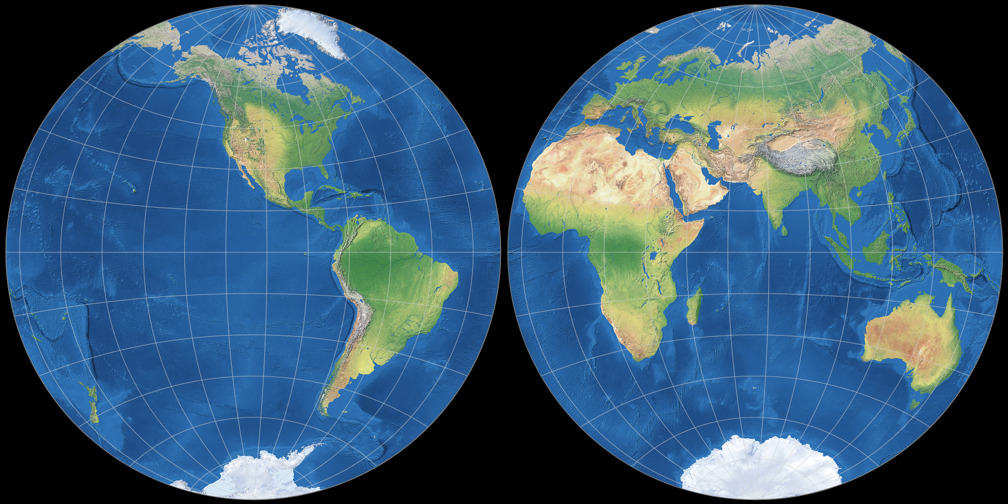
5. Comparison: Physical Map – scaled to same width
Breusing Harmonic
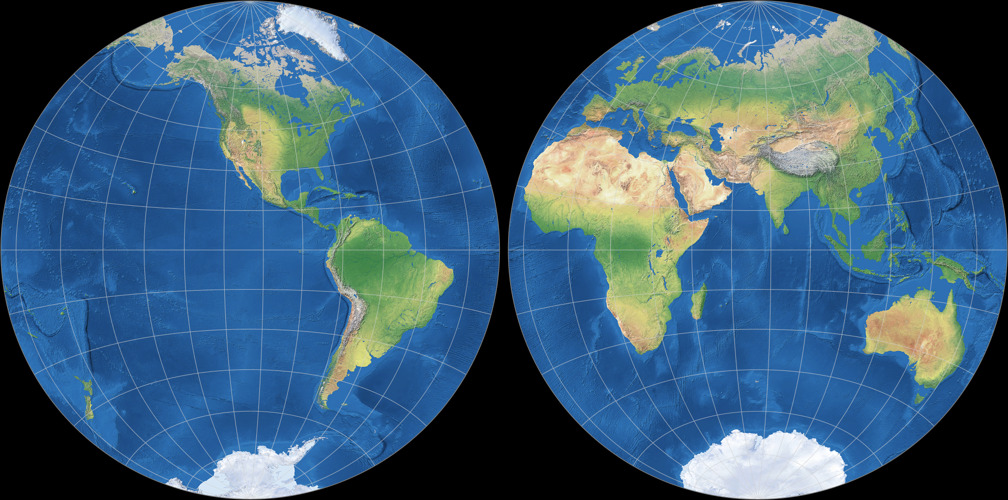
Nicolosi Globular
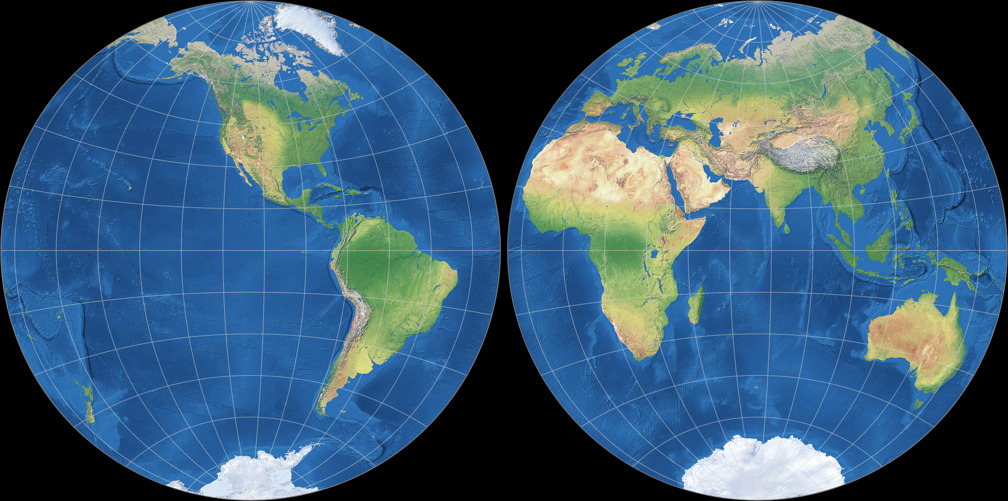
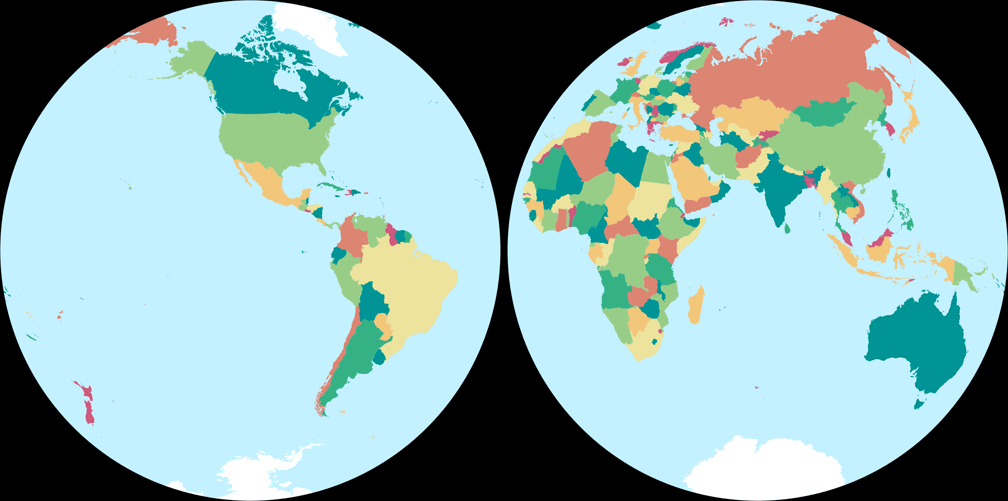
6. Comparison: Political Map – scaled to same width
Breusing Harmonic
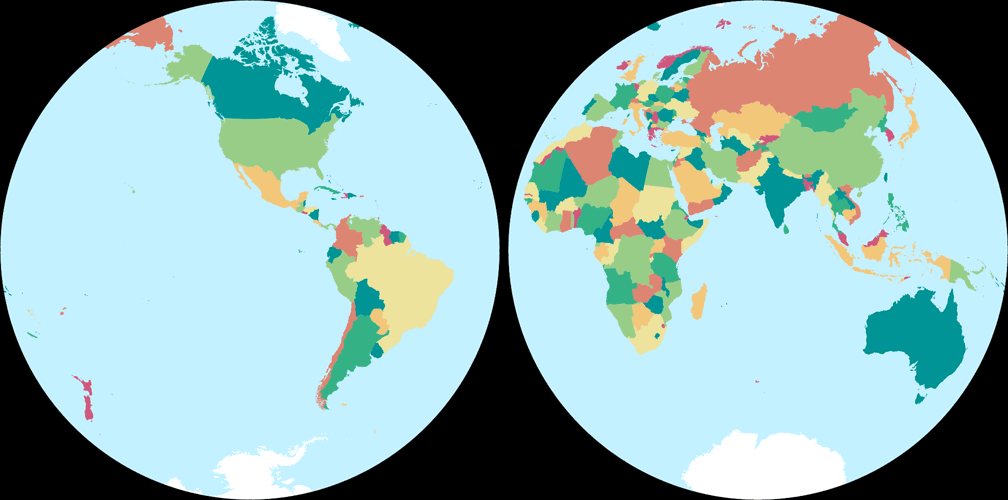
Nicolosi Globular
7. Comparison: Silhouette Map – scaled to same width
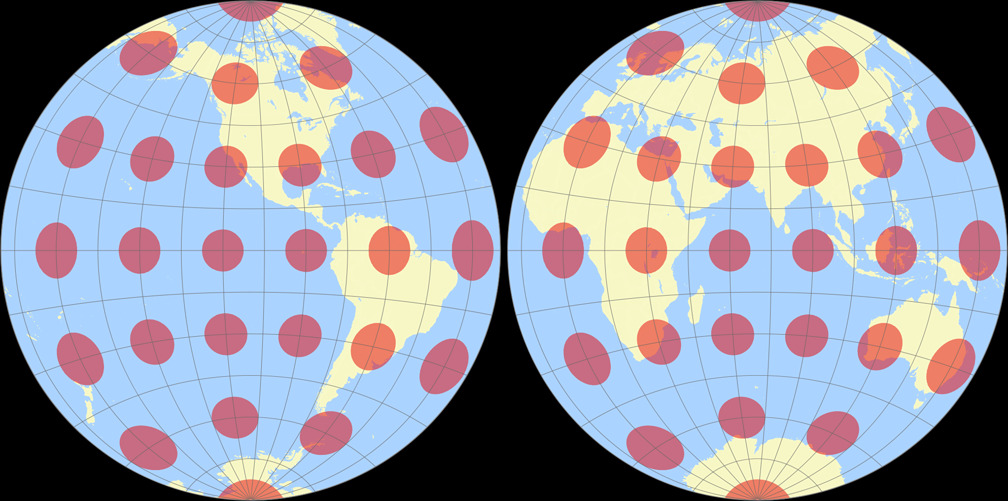
8. Comparison: Tissot Indicatrix, 30° – scaled to same width
Breusing Harmonic
Nicolosi Globular
9. Comparison: Tissot Indicatrix, 15° – scaled to fit
Breusing Harmonic
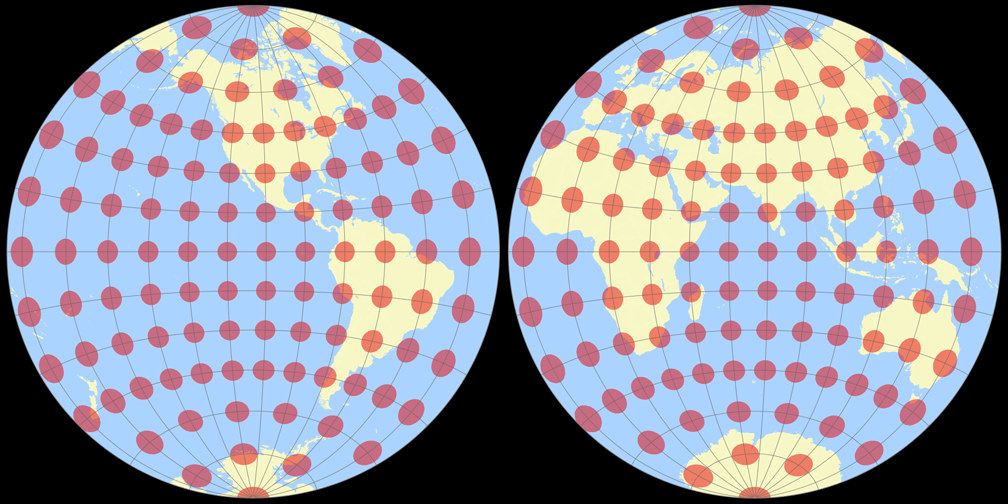
Nicolosi Globular
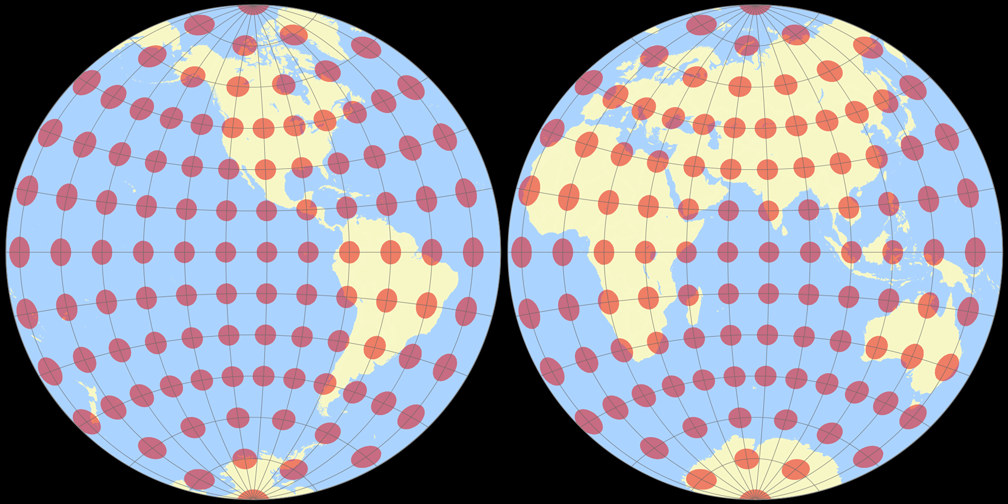
10. Comparison: Tissot Indicatrix, 15° – scaled to same width
Breusing Harmonic
Nicolosi Globular