My Projection Collection:
Compare Projections
Azimuthal equal-area (Hem.) vs. Ginzburg II
| Azimuthal equal-area (Hem.) | Ginzburg II | |
|---|---|---|
| Creator | Johann Heinrich Lambert (1772) | G.A. Ginzburg (1949) |
| Group | Azimuthal | Azimuthal |
| Property | Equal-area | Compromise |
| Other Names |
|
— |
| Remarks | — | A modification of the azimuthal equal-area projection. See my blogpost Two Ginzburg and four Baranyi Projections. |
| recommended comparisons | Ginzburg I Ginzburg II |
Azimuthal equal-area (Hem.) Ginzburg I |
|
This pairing is among the list of recommended pairings – but why? While very much alike at first glance, in direct comparision the differences become quite obvious. |
||
Remark: On these two projections, »scaled to fit« and »scaled to same width« will be quite identical!
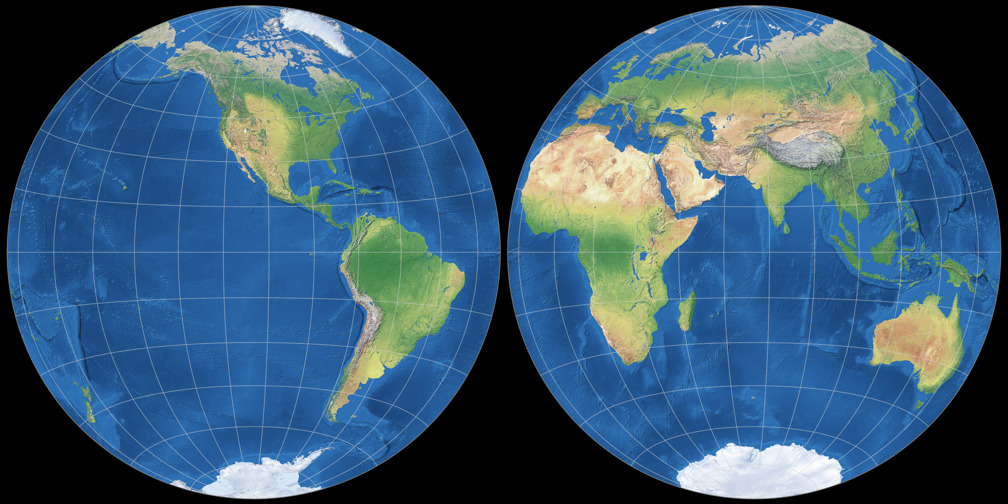
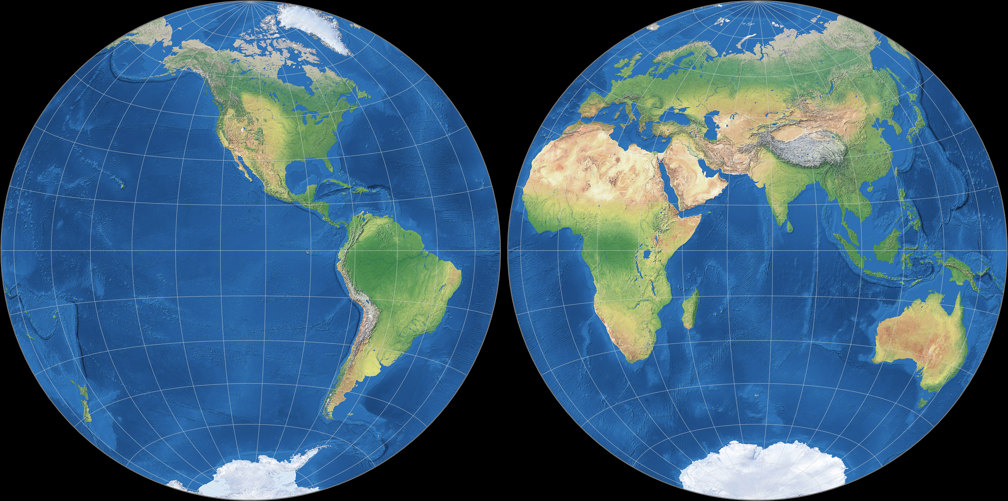
1. Comparison: Physical Map – scaled to fit
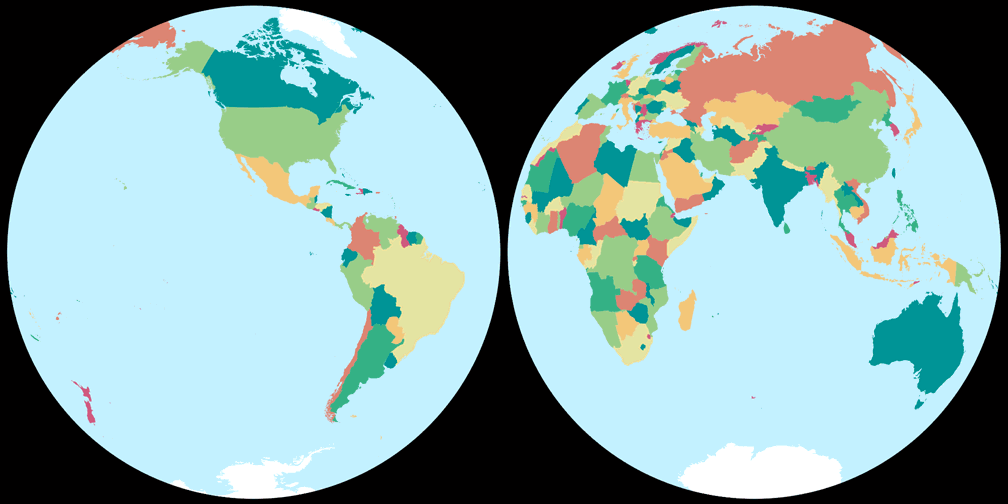
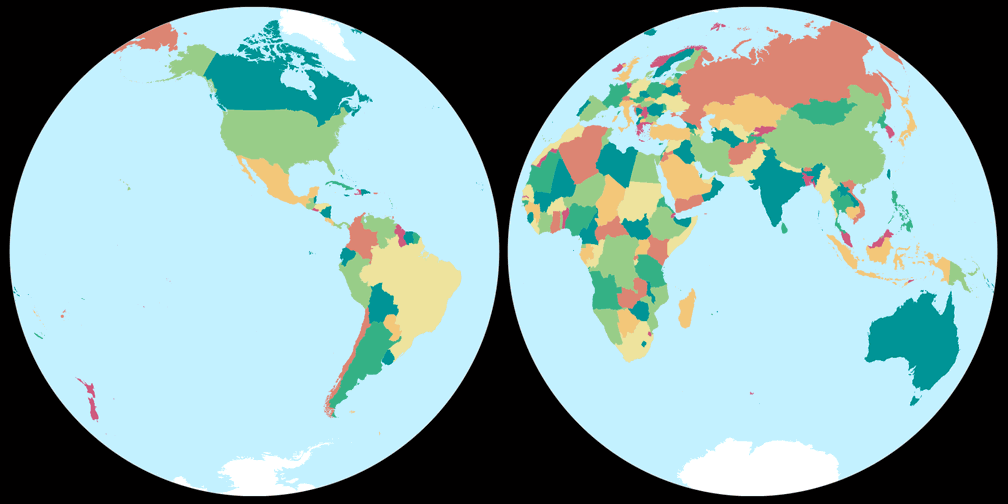
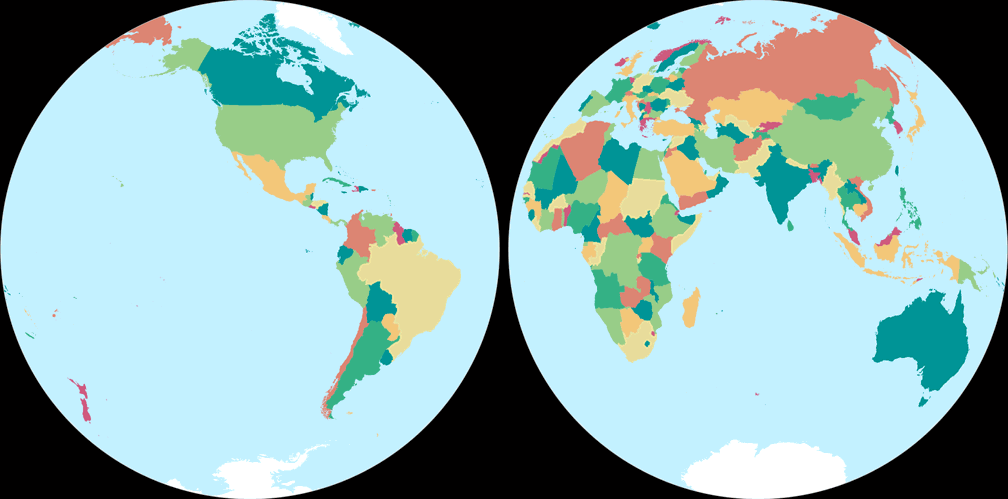
2. Comparison: Political Map – scaled to fit
Azimuthal equal-area (Hem.)
Ginzburg II
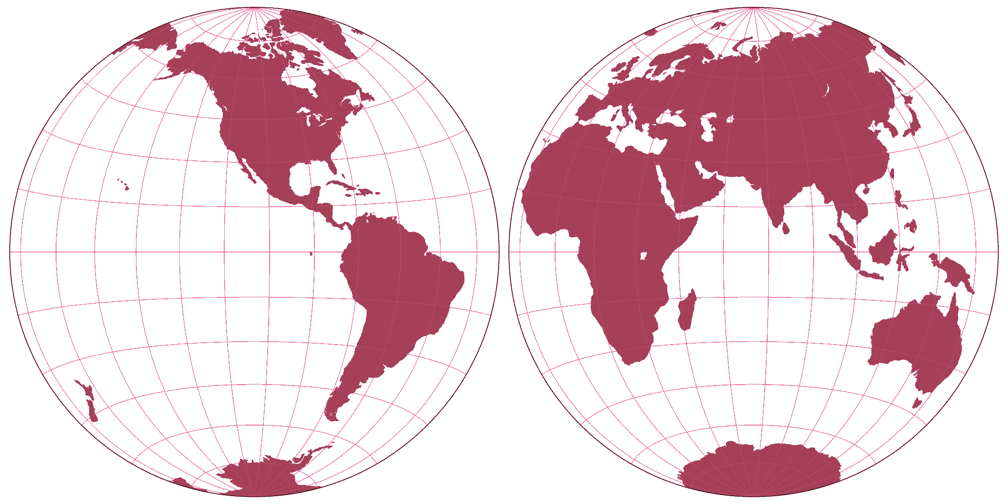
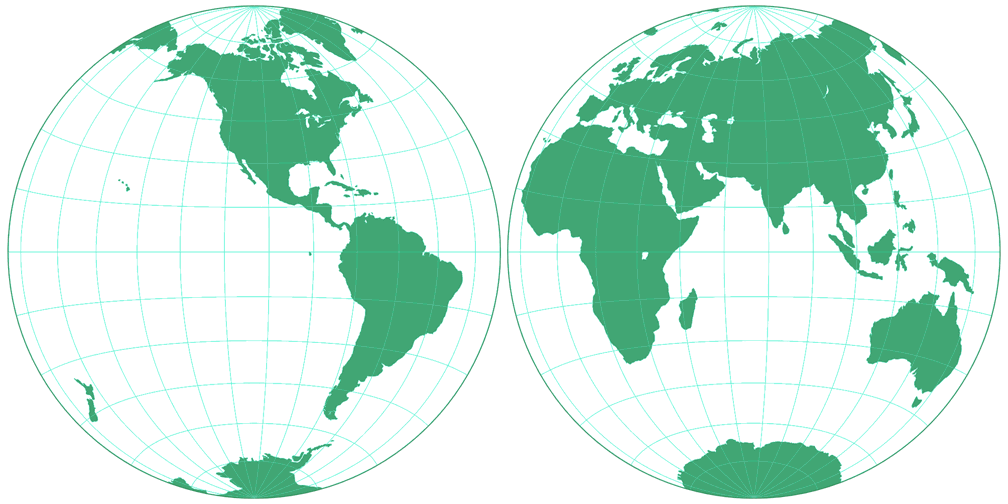
3. Comparison: Silhouette Map – scaled to fit
4. Comparison: Tissot Indicatrix, 30° – scaled to fit
Azimuthal equal-area (Hem.)
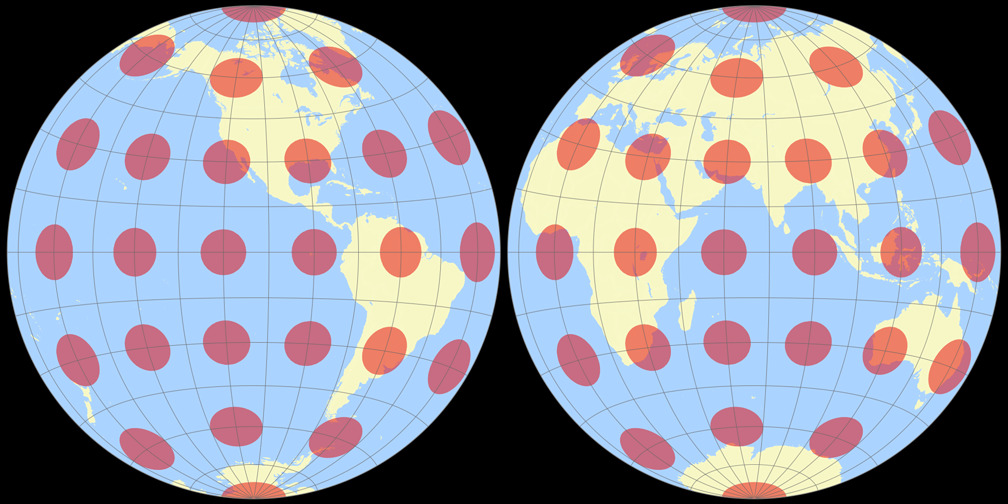
Ginzburg II
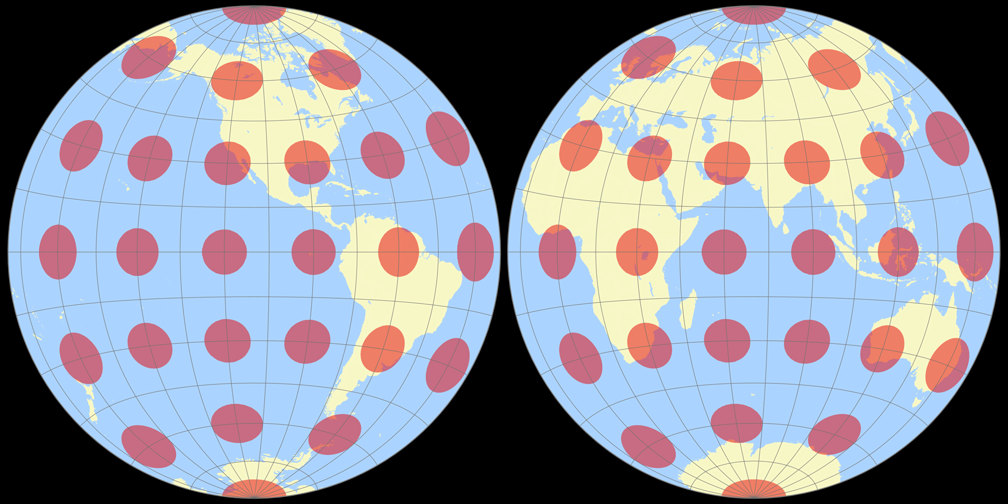
Azimuthal equal-area (Hem.) Tissot Indicatrix c Tobias Jung
Ginzburg II Tissot Indicatrix c Tobias Jung
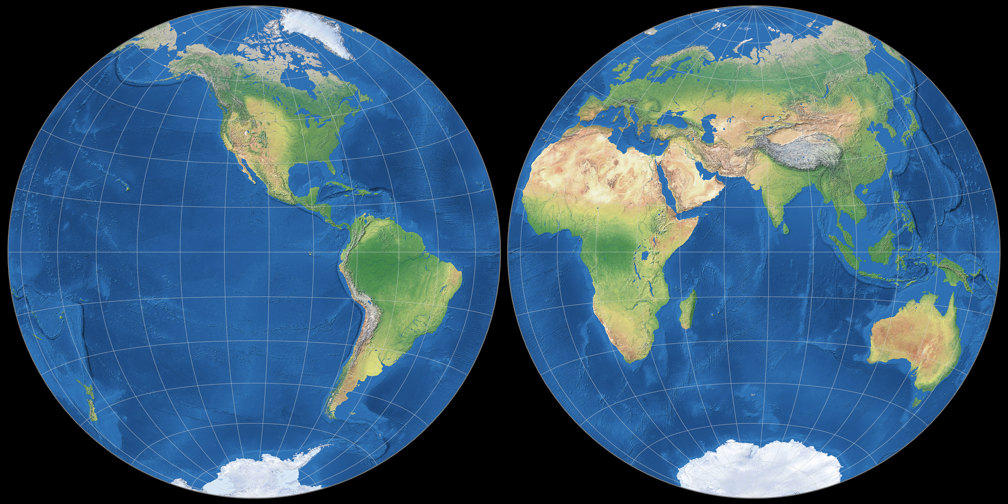
5. Comparison: Physical Map – scaled to same width
Azimuthal equal-area (Hem.)
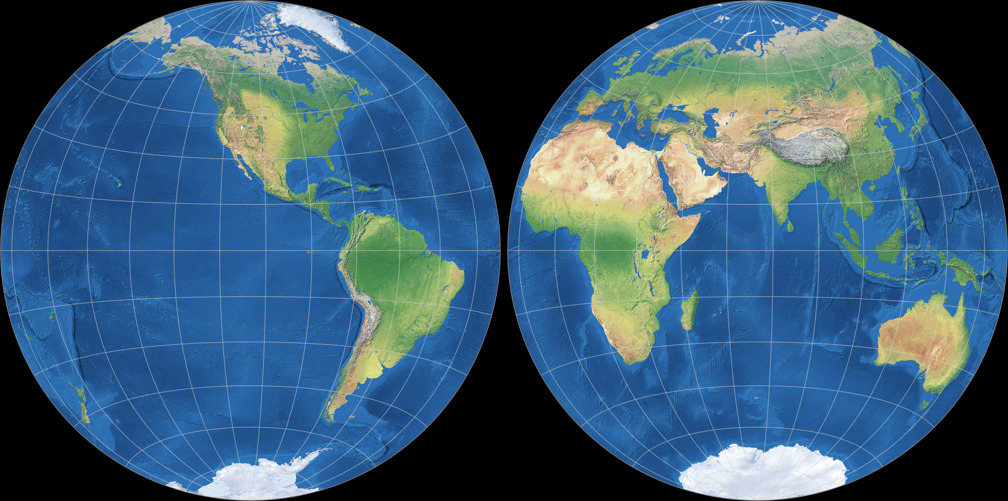
Ginzburg II
6. Comparison: Political Map – scaled to same width
Azimuthal equal-area (Hem.)

Ginzburg II
7. Comparison: Silhouette Map – scaled to same width
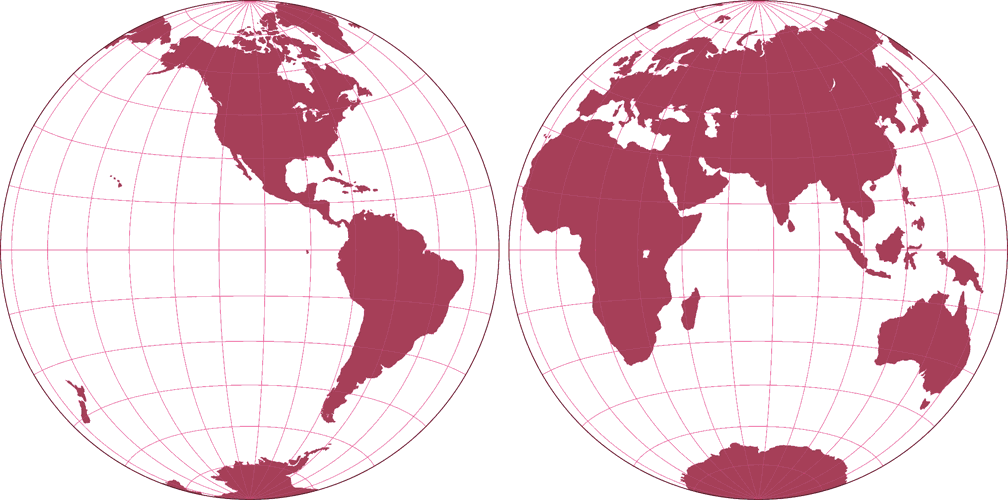
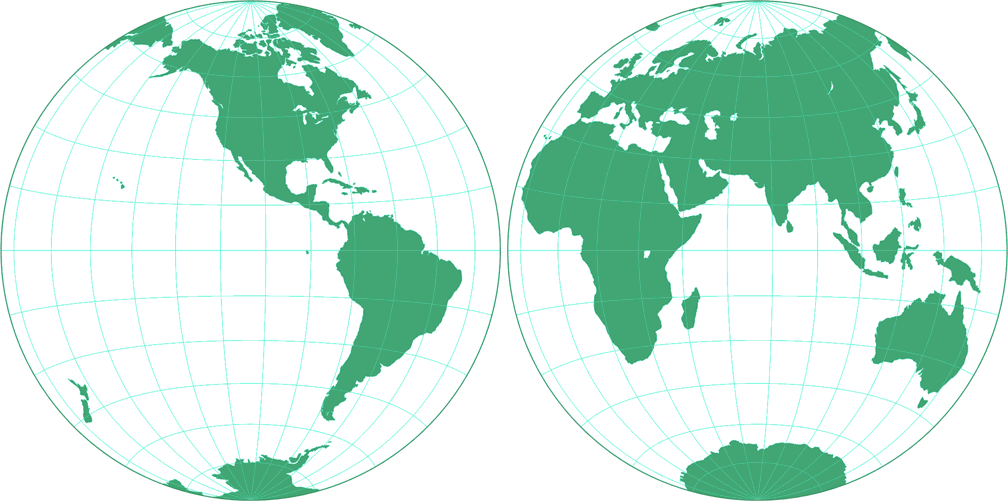
8. Comparison: Tissot Indicatrix, 30° – scaled to same width
Azimuthal equal-area (Hem.)
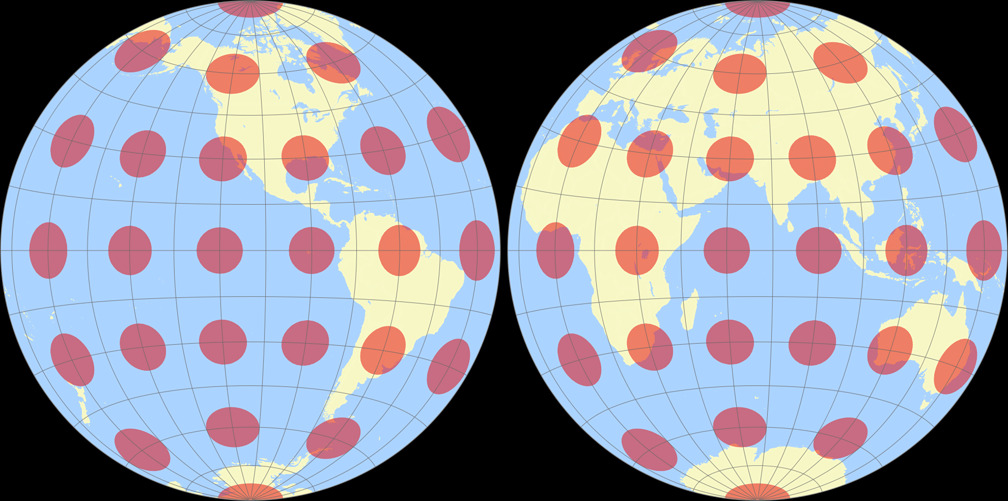
Ginzburg II
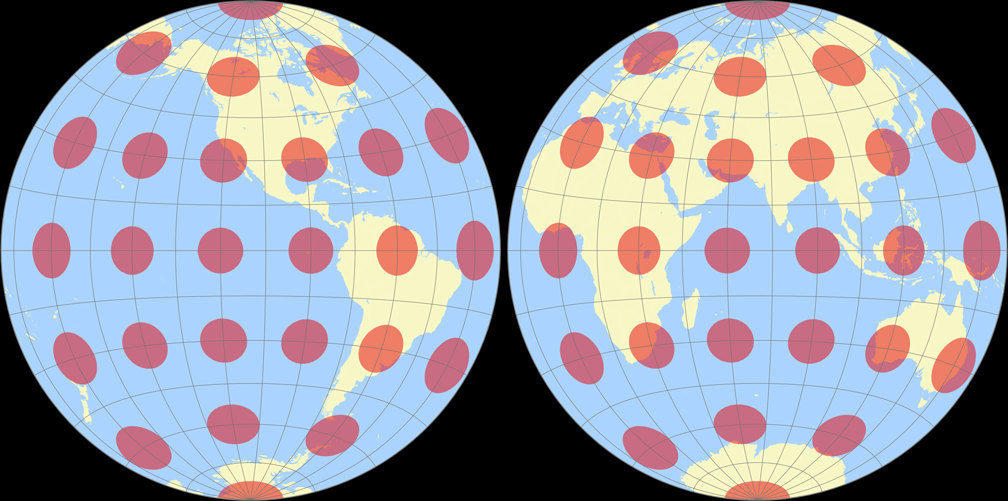
Azimuthal equal-area (Hem.) Tissot Indicatrix c Tobias Jung
Ginzburg II Tissot Indicatrix c Tobias Jung
9. Comparison: Tissot Indicatrix, 15° – scaled to fit
Azimuthal equal-area (Hem.)
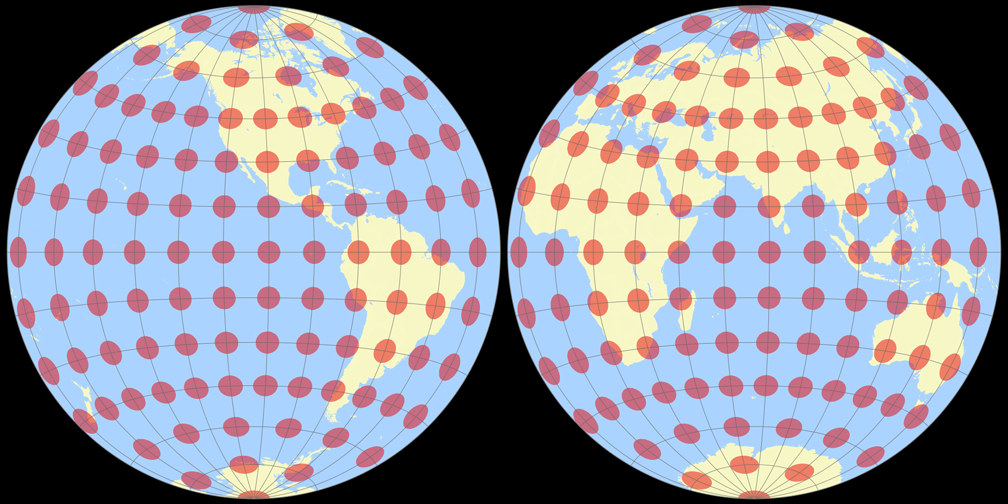
Ginzburg II
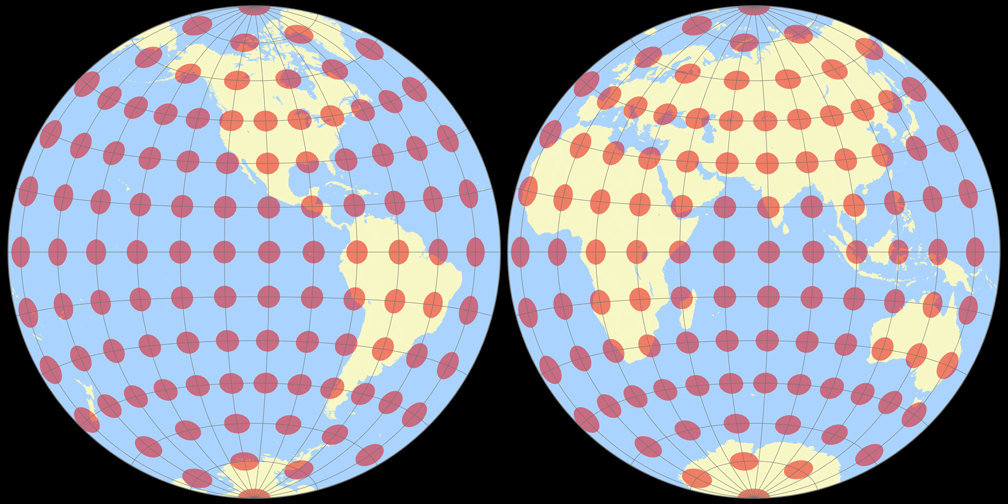
Azimuthal equal-area (Hem.) Tissot Indicatrix c Tobias Jung
Ginzburg II Tissot Indicatrix c Tobias Jung
10. Comparison: Tissot Indicatrix, 15° – scaled to same width
Azimuthal equal-area (Hem.)
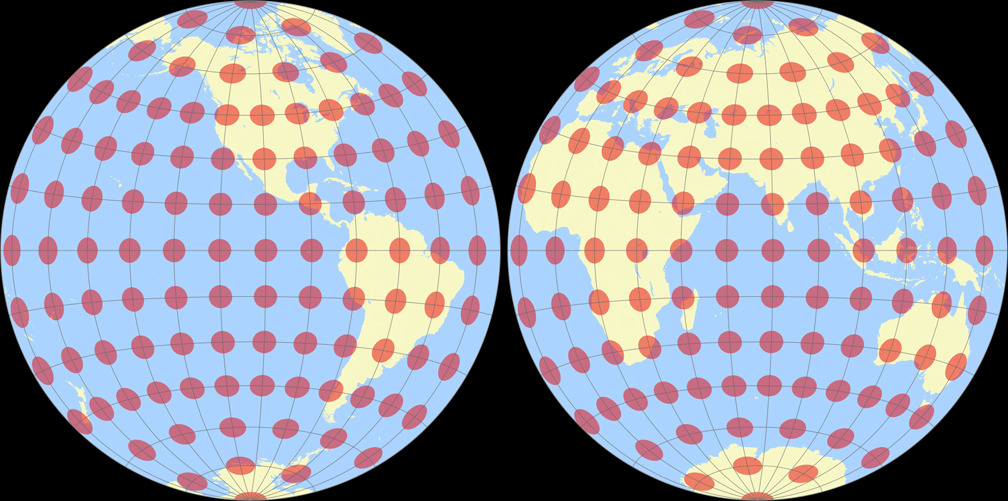
Ginzburg II
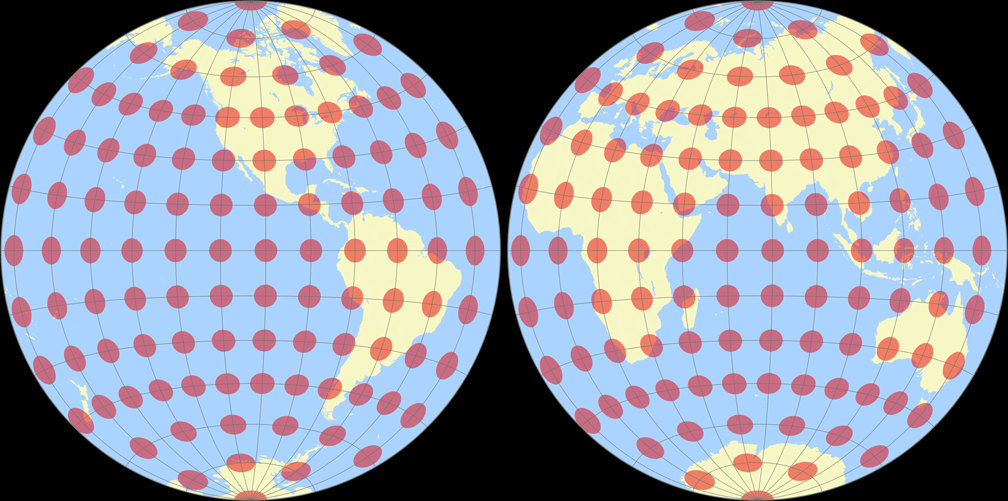
Azimuthal equal-area (Hem.) Tissot Indicatrix c Tobias Jung
Ginzburg II Tissot Indicatrix c Tobias Jung