My Projection Collection:
Compare Projections
Winkel-Denner I (50.46°) vs. Winkel Tripel
| Winkel-Denner I (50.46°) | Winkel Tripel | |
|---|---|---|
| Creator | Peter Denner (2023) | Oswald Winkel (1921) |
| Group | Lenticular | Lenticular |
| Property | Compromise | Compromise |
| Other Names |
|
|
| Remarks | Arithmetic mean of the equirectangular (with φ0 ≈ 50°28´) and Aitoff projections for the x values, and of the equirectangular and (scaled up) Hammer projections for the y values. Originally presented in a thread in the mapthematics forum. Also see the blogpost The Winkel-Denner Projections. |
— |
| recommended comparisons | — | Ciric I Natural Earth II Wagner IX.i Winkel Tripel Bartholomew Winkel Tripel BOPC |
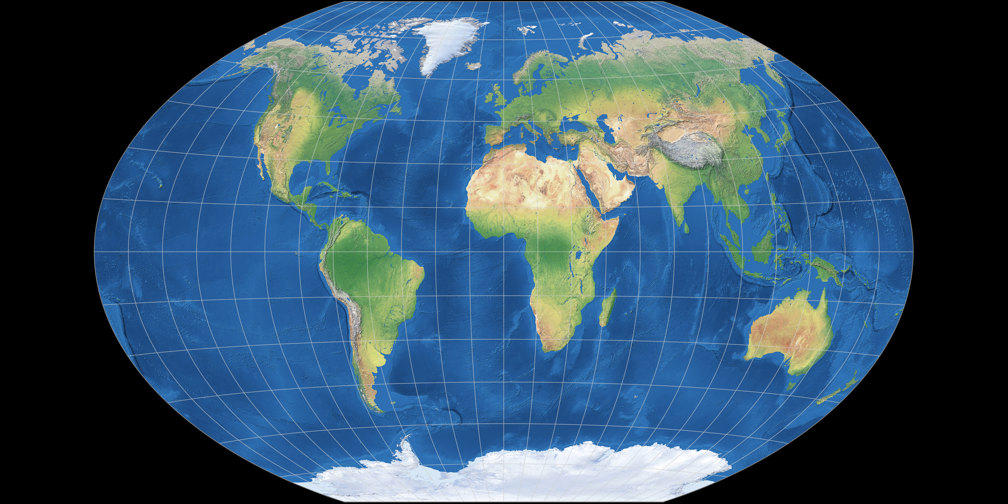
1. Comparison: Physical Map – scaled to fit
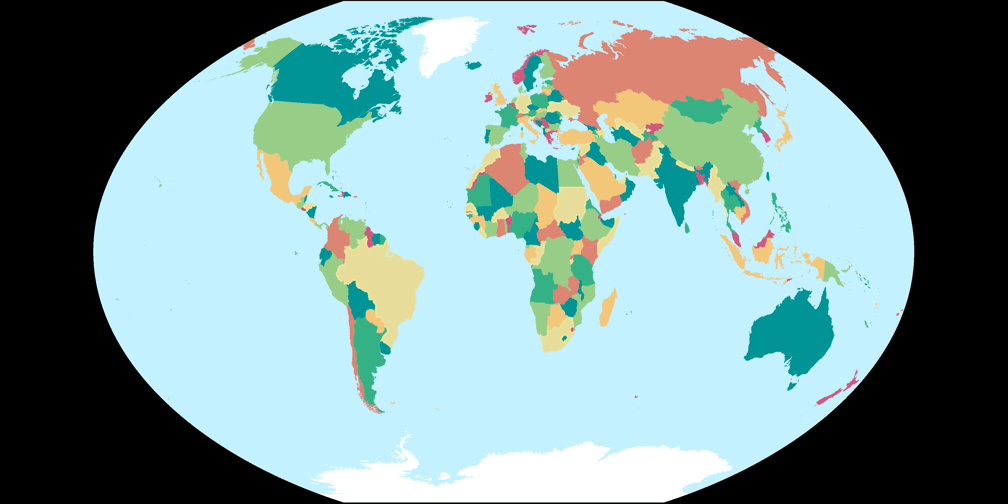
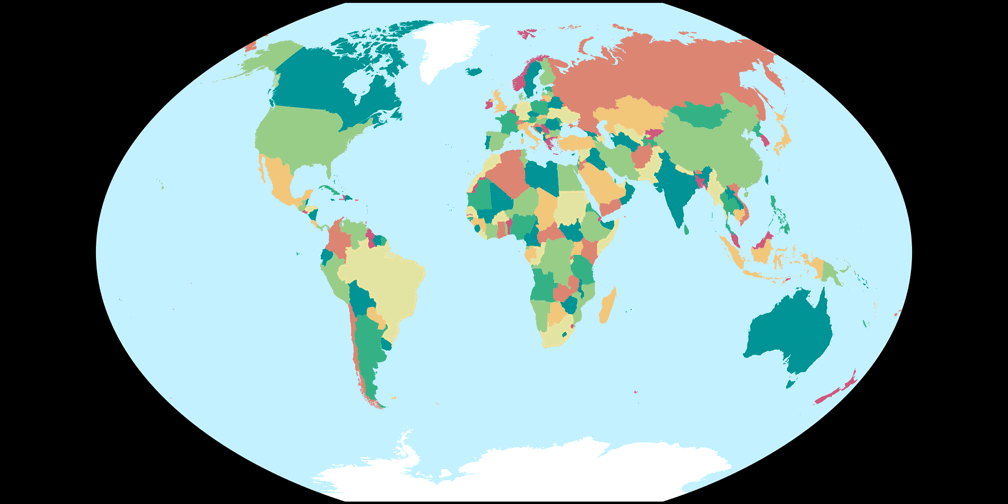
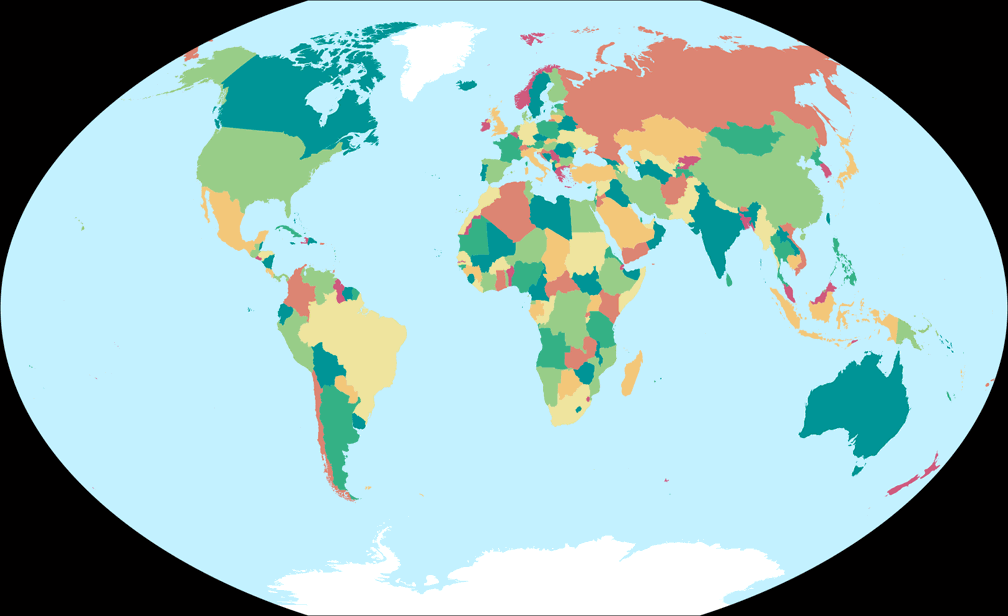
2. Comparison: Political Map – scaled to fit
Winkel-Denner I (50.46°)
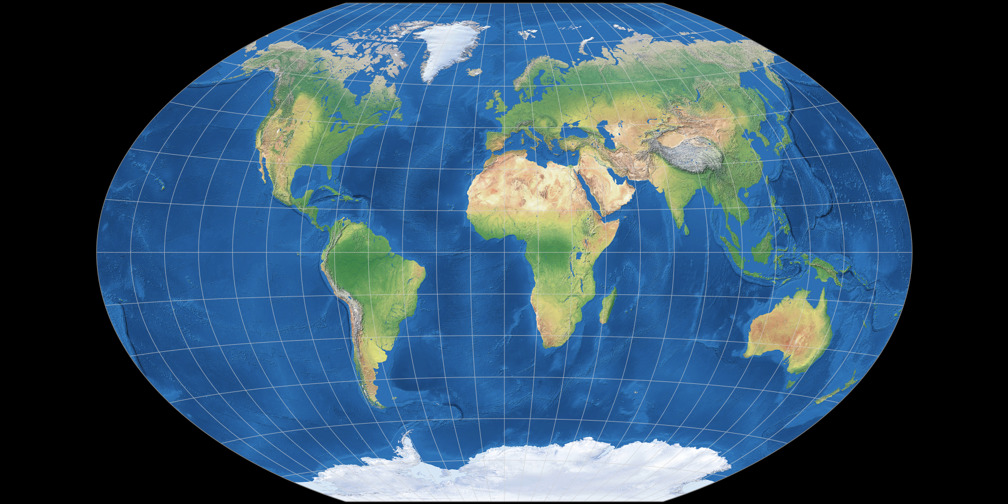
Winkel Tripel
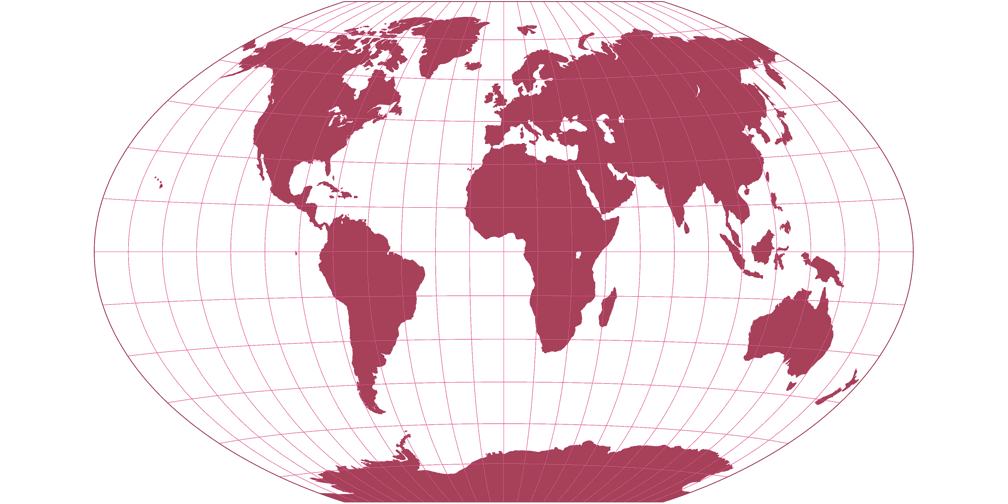
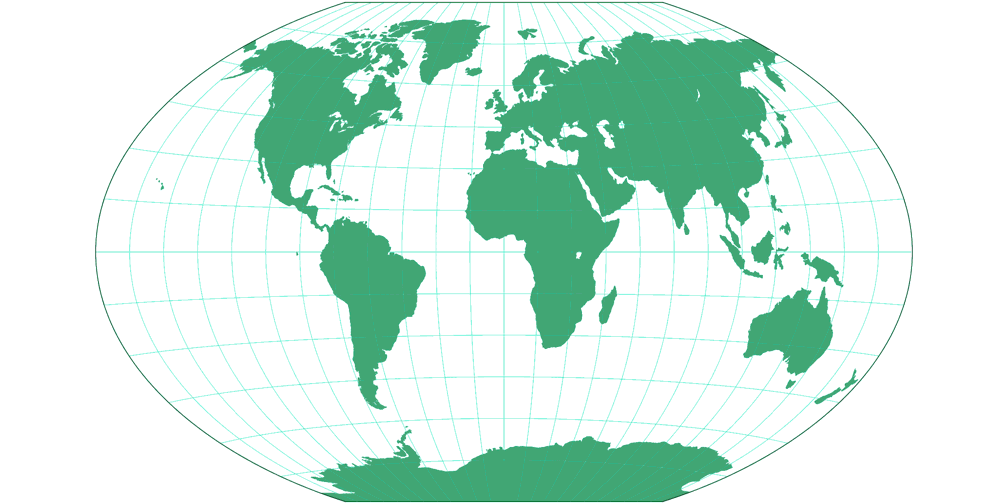
3. Comparison: Silhouette Map – scaled to fit
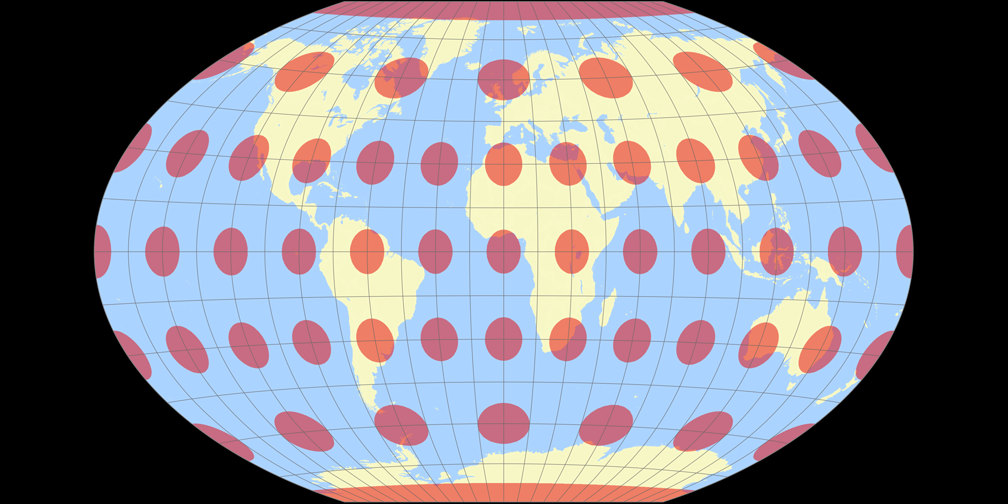
4. Comparison: Tissot Indicatrix, 30° – scaled to fit
Winkel-Denner I (50.46°)
Winkel Tripel
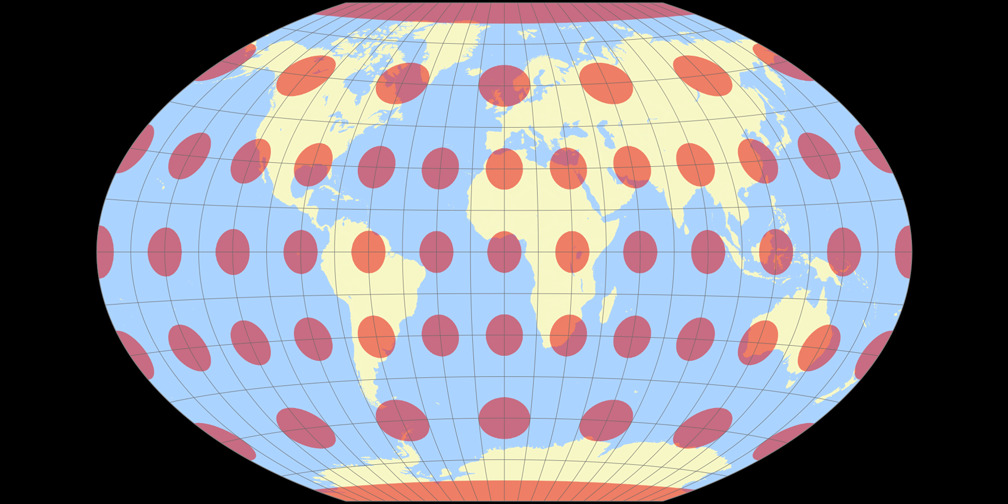
Winkel-Denner I (50.46°) Tissot Indicatrix c Tobias Jung
Winkel Tripel Tissot Indicatrix c Tobias Jung
5. Comparison: Physical Map – scaled to same width
Winkel-Denner I (50.46°)
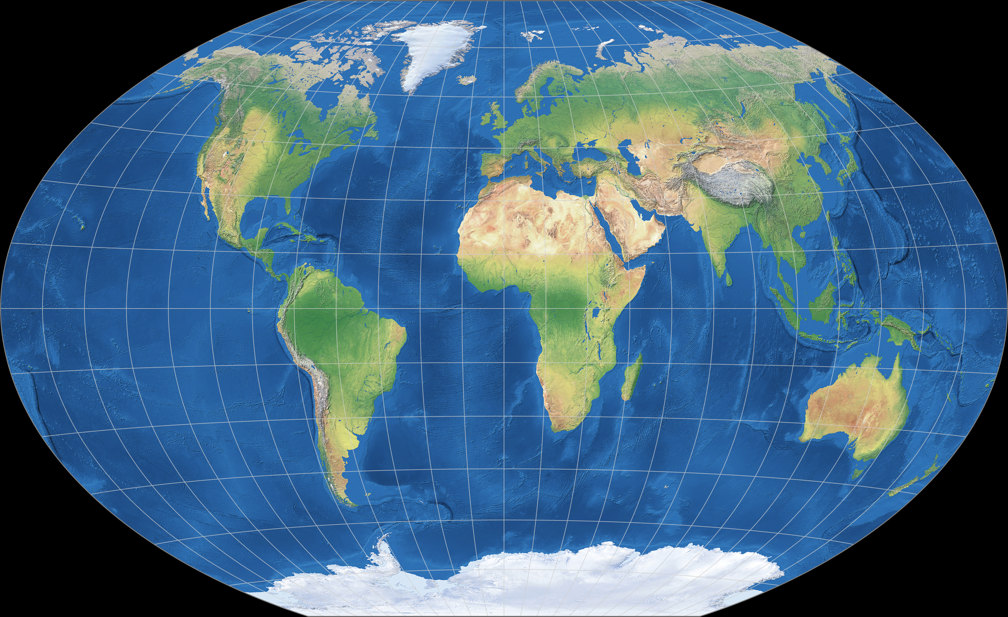
Winkel Tripel
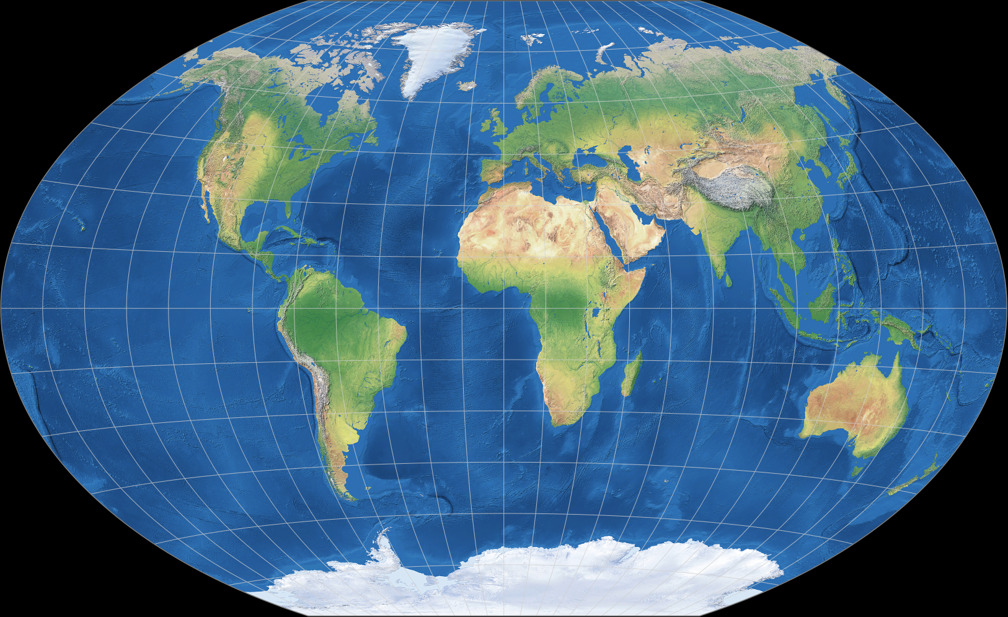
6. Comparison: Political Map – scaled to same width
Winkel-Denner I (50.46°)
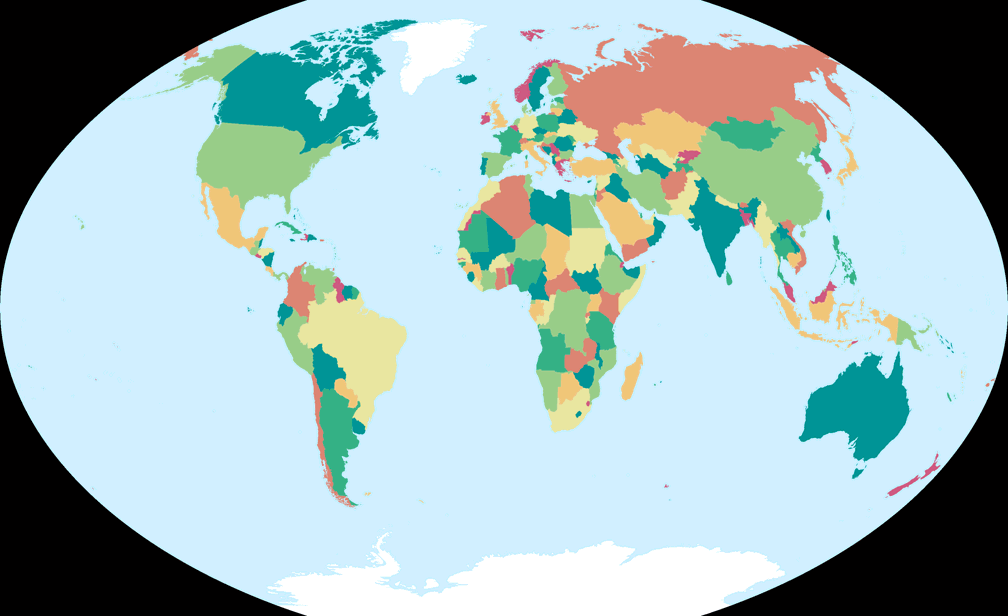
Winkel Tripel
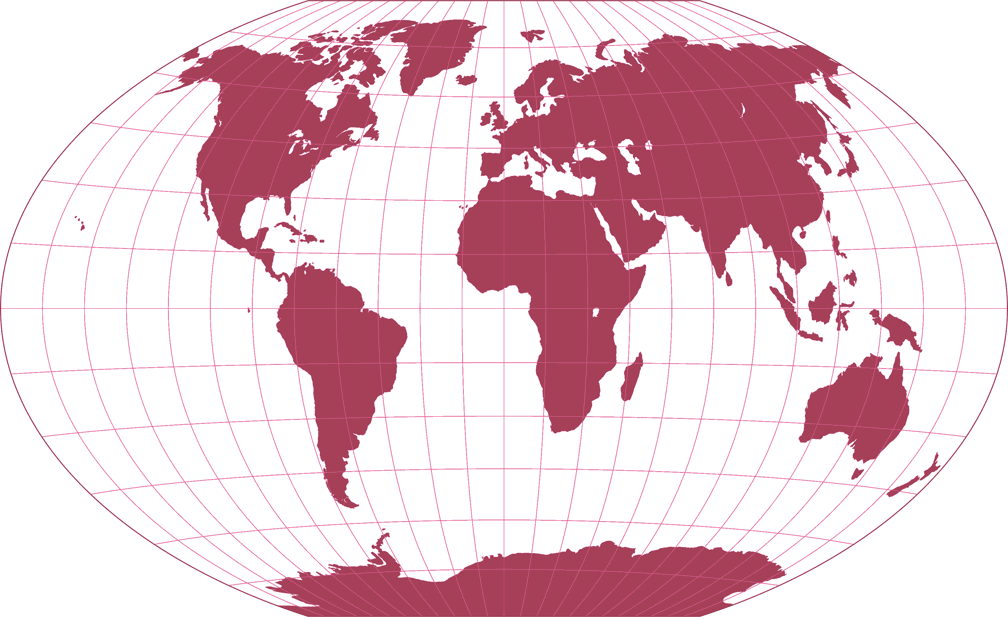
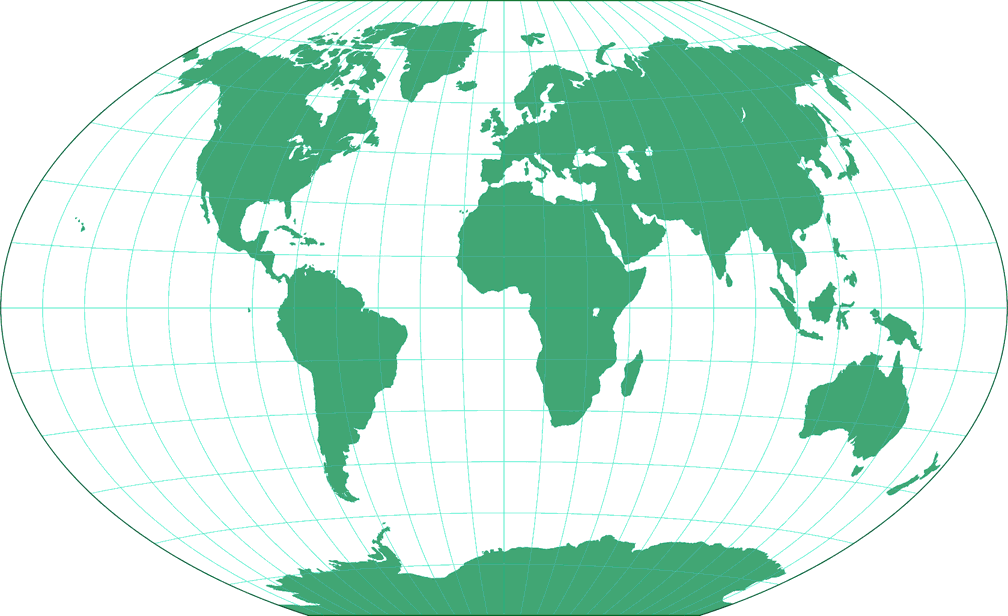
7. Comparison: Silhouette Map – scaled to same width
8. Comparison: Tissot Indicatrix, 30° – scaled to same width
Winkel-Denner I (50.46°)
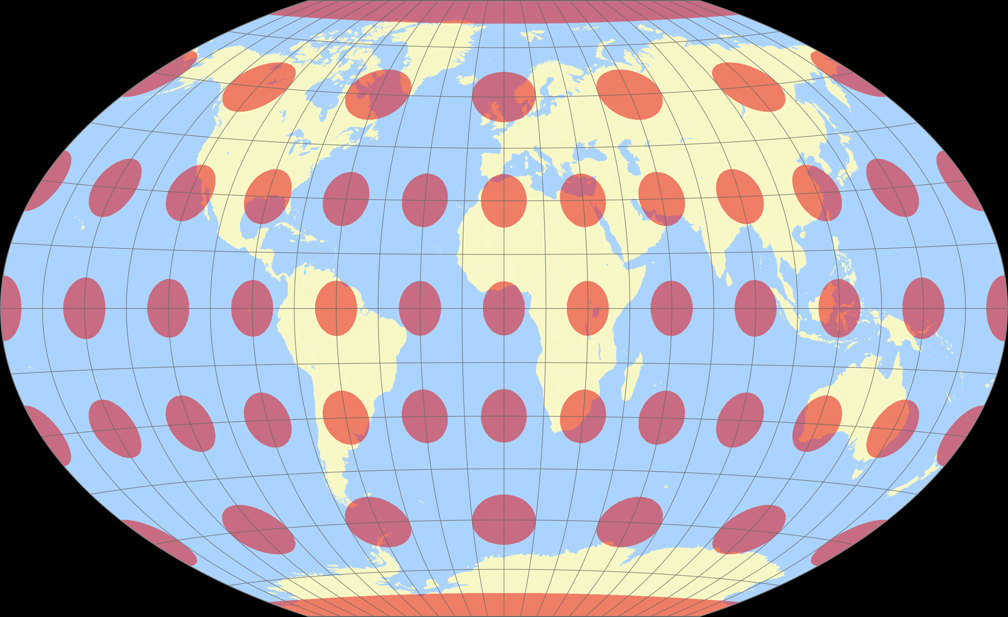
Winkel Tripel
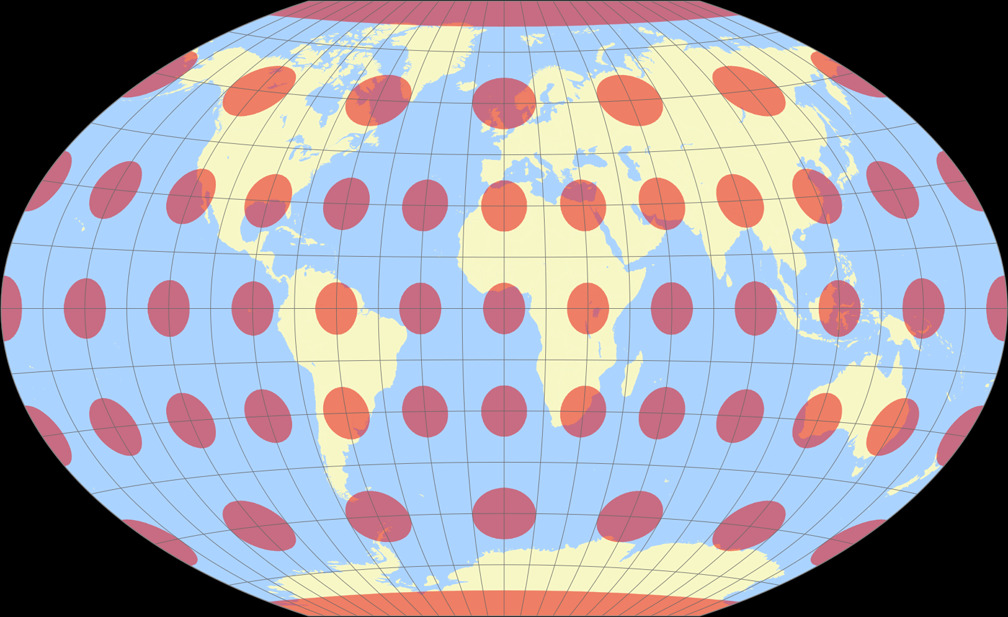
Winkel-Denner I (50.46°) Tissot Indicatrix c Tobias Jung
Winkel Tripel Tissot Indicatrix c Tobias Jung
9. Comparison: Tissot Indicatrix, 15° – scaled to fit
Winkel-Denner I (50.46°)
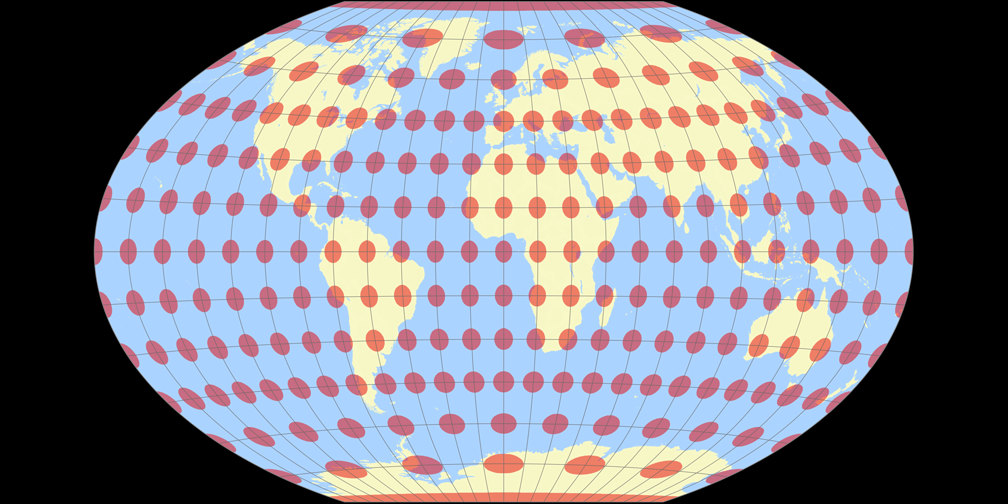
Winkel Tripel
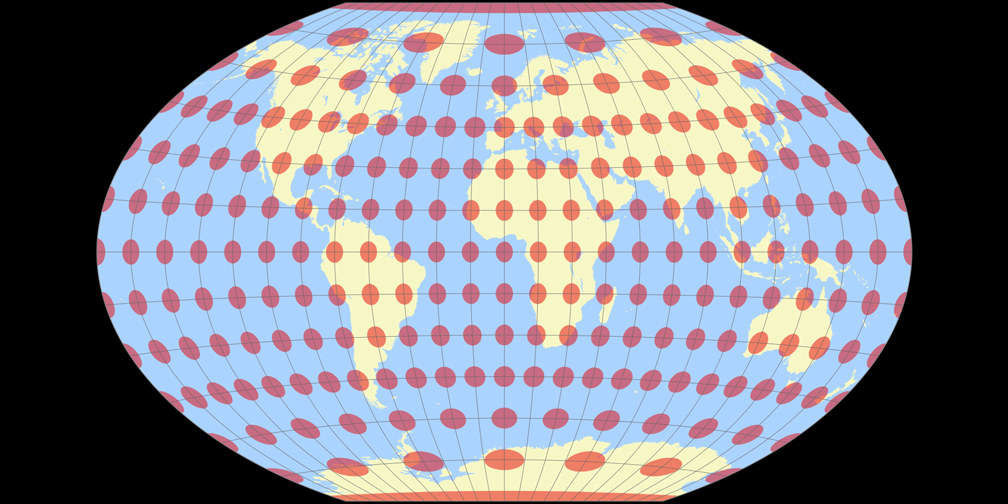
Winkel-Denner I (50.46°) Tissot Indicatrix c Tobias Jung
Winkel Tripel Tissot Indicatrix c Tobias Jung
10. Comparison: Tissot Indicatrix, 15° – scaled to same width
Winkel-Denner I (50.46°)
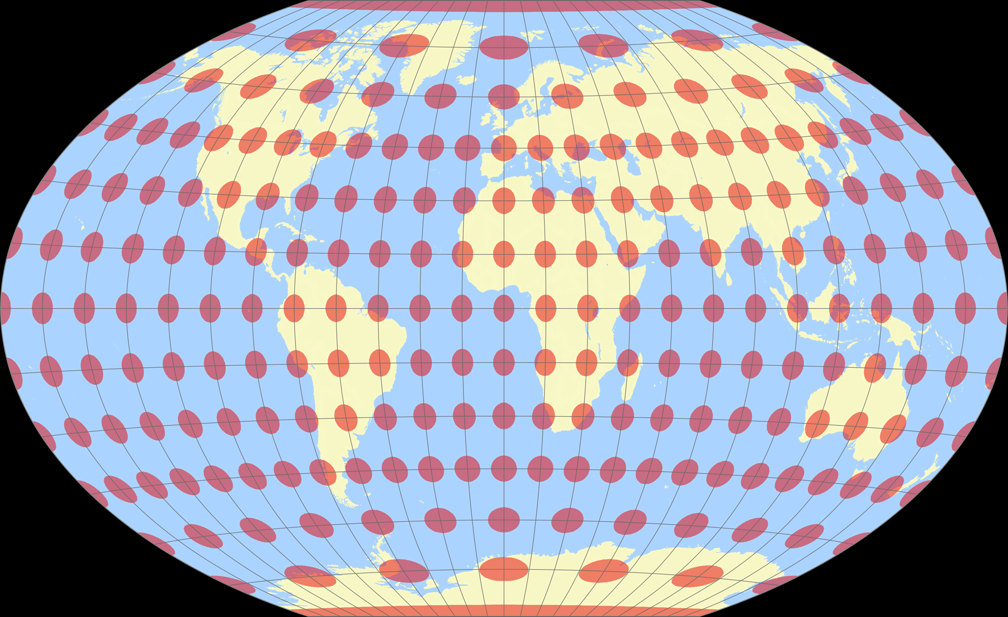
Winkel Tripel
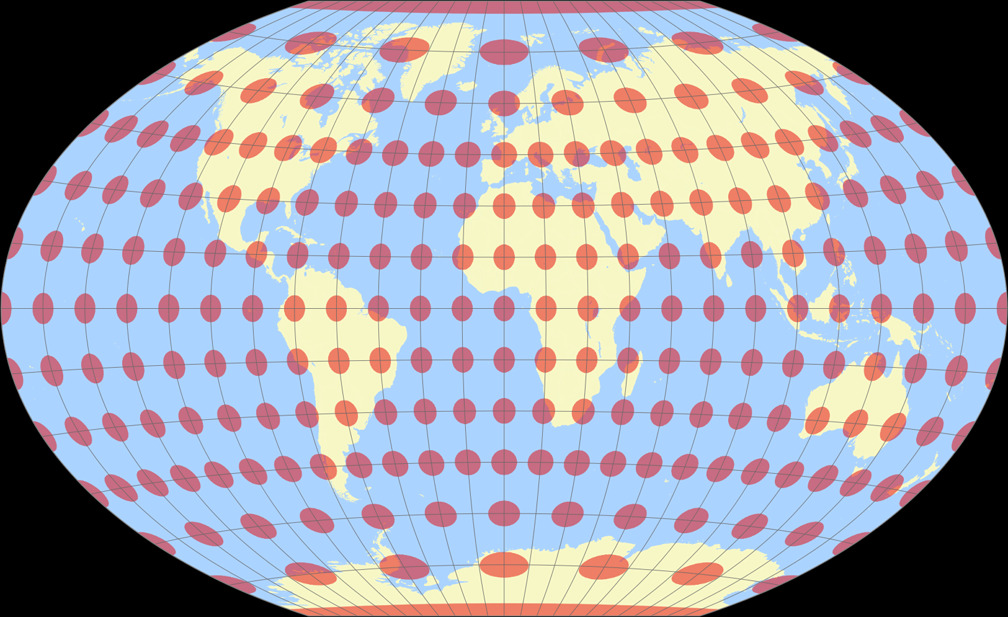
Winkel-Denner I (50.46°) Tissot Indicatrix c Tobias Jung
Winkel Tripel Tissot Indicatrix c Tobias Jung