Compare Map Projections

Deutsch  •  English
—
[info]    Viewing options:      

What’s a Map Projection? – A brief introduction

208px GEO Globe
CC BY-SA Christian Fischer

The Earth is a sphere.
(Well, not exactly, but close enough.)
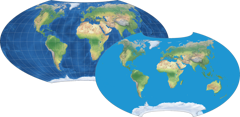
The only accurate representation of the Earth’s surface is to be found on a globe.

A globe show you the Earth as it it – reduced in size for practical reasons since most people lack space to place a globe that is roughly 12,742 kilometers (7,918 mi) in diameter on their desktop.
But shape and proportions of the land masses and oceans, their position relative to each other, are shown correctly.

But sadly, it’s impossible to show the surface of the Earth accurately on a flat map, which was proven mathematically by Leonhard Euler in 1777. A common real world example is to imagine peeling an orange and pressing the orange peel flat on a table: The peel would bulge and break.

PD KoenB

So this isn’t working and therefore people resorted to projections:
Imagine Earth to be translucent. Imagine you have a light source and a big (really big!) piece of paper which is wrapped around the Earth and serves as screen which caputeres the image that is thrown by the light source.

Have a look at the schematic illustration of the set-up.
I should make clear how a map projection (in theory) works, and why it is called projection after all. And if you look at Greenland (the lilac island at the top of the globe and the map) you see the distortion of shape.

But the illustration is showing only one possible way to capture the image.
Depending on where exactly you place the light source, the way you wrap the piece of paper around the Earth (if you do that at all, for you might also place it flat besides the Earth), where the screen touches the Earth (if at all), a totally different image might be captured. And in that image, maybe Greenland isn’t distorted, but Africa is.

But most importantly, most projections doesn’t even work that way!
You cannnot construct them like that, they are build purely mathematically instead. But they are called projections nonetheless.

So you have a vast range of different ways to project the Earth’s surface to flat map, however one problem remains:

You can’t show the Earth accurately, so you try to show it approximately. You are forced to stretch some parts of the surface, compress others, maybe bend them some. That leads to distortions.
It is important to remember that each and every world map has some kind of distortion!

But you can distort different parts if the Earth, you can choose different kinds of distortion. A specific combination of these possibilities is called a projection. And there are hundreds of different projections, each one with its own kind and positioning of distortion, in a lot of different shapes.

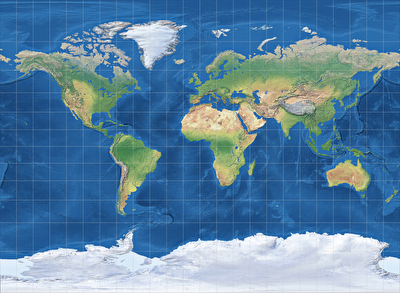
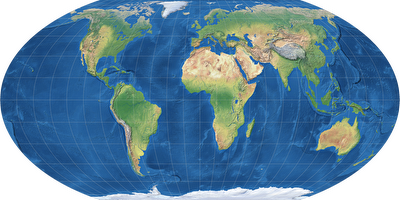
Miller 400 Wagner 4 400
 
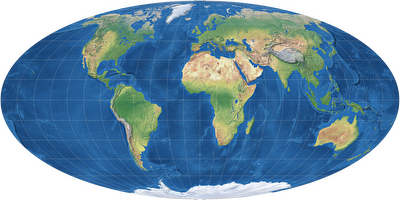
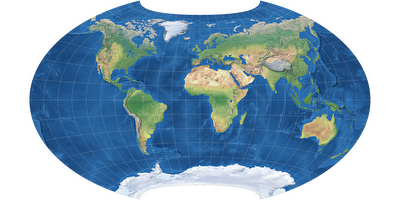
Mollweide 400 Canters W13 400
 
Left to right, top to bottom: Miller, Wagner IV, Mollweide, Canters W14.
 

And none of them is really accurate, none is wrong, none is better or worse than the others in itself. They are different, they serve different purposes, they aim to emphasise different aspects.

Nonetheless, you might choose the wrong projection for a special presentation – but only because it’s the wrong one for this very purpose. In other circumstances, the »wrong« projection might even be the best choice.

Back to Basic Knowledge  •  Go to top

Comments

3 comments
There are further comments in the german version.

characters remaining: 2048
  
X Icon

Please leave the following four input field blank in any case!

Oguz Kupusoglu

Thank you very much for the web site! It contains a lot of information and its design is very nice.
Wed June 08, 2016 11:41 am CEST
characters remaining: 2048
  
X Icon

Please leave the following four input field blank in any case!

Ken Stallcup

I was chatting with Facebook friends about map projections, did a search and found your site. I'm going to pass it along to them as well as to save it and study it myself. Excellent site! Thanks!
Tue Nov 17, 2020 5:39 am CET
characters remaining: 2048
  
X Icon

Please leave the following four input field blank in any case!

Alexandre Canana

Mr Jung, I would like to know, if you could enlighten me, if the Erdi-Krauz projection is equal area?
Wed Dec 22, 2021 7:09 pm CET   –    101 replies

Tobias Jung

Hello,

the Erdi-Krausz projection is a fusion of two projections: A flat-polar sinusoidal (between 60° N and S) and the Mollweide projection (poleward). Both projections are equal-area but at different scales. Therefore, the complete map is not equal-area.

And thanks for asking, which made me realize that I never added that bit in the projection information; I’ll fix this soon!
Thu Dec 23, 2021 12:18 pm CET

Alexandre Canana

No problem, I mean, you do classify it as a compromise or aphylatic projection.
Thu Dec 23, 2021 12:28 pm CET

Alexandre Canana

John Snyder even describes the flat-polar sinusoidal used and says that the Mollweide part was «necessarily enlarged» so I guess it's one reason why the complete map is not equal area. I suppose Erdi-Krauz had to do that for it to fit the flat-polar sinusoidal.
Thu Dec 23, 2021 12:34 pm CET

Alexandre Canana

Although when it comes to map projections, when it comes to combining them, I prefer the blending/arithmetical mean/averaging technique.
Thu Dec 23, 2021 12:37 pm CET

Alexandre Canana

Because the result will always be intermediate between the two projections involved, and so, it'll be better than either one in appearance while having less distortion and combining their advantages
Thu Dec 23, 2021 12:40 pm CET

Alexandre Canana

I love map projections and I really like your website!
Thu Dec 23, 2021 12:42 pm CET

Alexandre Canana

I suppose that was the reasoning behind the Boggs Eumorphic, because the Mollweide is bounded by an ellipse which is a shape that reflects the Earth's roundness and is very aestetically pleasing for that reason while having a skinny Africa because of the equatorial stretching it has. The classic Sinusoidal does have a better equator because it has no shape nor angular distortion at the intersection of the equator with the central meridian but the poles are too sharp and everything far away from the equator looks it's getting into a vaccum cleaner. So probably Boggs liked both advantages of both projections and exactly took the mean of the y-coordinate and the harmonic mean of the x-scale to maintain equal area in the resulting projection because the more commonly used linear combination or averaging at least generally, wouldn't produce an equal area result
Thu Dec 23, 2021 2:30 pm CET

Alexandre Canana

Basically, fused projections are joined where the scale is the same and each projection is used where it has less distortion. And blended projections combine two projections that can be joined without any bizarre singularities like overlaps, loops or holes, and try to combine the advantages of both designs while reducing the both of their distortion.
Thu Dec 23, 2021 3:05 pm CET

Tobias Jung

Yes, blending avoids these problems – and Winkel proofed that you can get excellent results using this technique. However, fusing projections can be advantageous, too; e.g. the Strebe Asymmetric 2011 is a fusion of two projections and I think it achieves its goal (to reduce angular distortions on the continental areas while retaining equivalence) very well.
Thu Dec 23, 2021 3:56 pm CET

Alexandre Canana

Yeah, I like fused projections as long as they don´t look too weird like the uninterrupted Goode Homolosine, for example. For example the Erdi-Krauz is not too much different from the Mollweide except for being only equal area in a limited sense(at two scales)and having a slight break in it.
Thu Dec 23, 2021 6:47 pm CET

Alexandre Canana

Well, all projections are interrupted, but you know what I mean by that.
Thu Dec 23, 2021 6:49 pm CET

Tobias Jung

Yes, of course I know what you mean. :-)
After all, I listed “interrupted” projections for a long time as own group here on my website. Later, I filed them under their real group (i.e. pseudocylindrical for most of them).
Thu Dec 23, 2021 7:17 pm CET

Alexandre Canana

And you're right, the Strebe 1995 and it's 2011 «Relative» are amongst the most elegant and pleasing equal area projections, besides the Mollweide, the Hammer-Wagner and the Hammer-Aitoff to name a few.
Thu Dec 23, 2021 7:48 pm CET

Alexandre Canana

I also really like your own equivalent projections
Thu Dec 23, 2021 7:55 pm CET

Alexandre Canana

Along with the ones that aren't.
Thu Dec 23, 2021 7:56 pm CET

Alexandre Canana

Meaning your non equal area projections.
Thu Dec 23, 2021 7:57 pm CET

Tobias Jung

Thank you! :-)
By the way, I’m going to add a few own equal-area fusions soon. (Well, that is… probably not before the end of January or something…)
Thu Dec 23, 2021 8:00 pm CET

Alexandre Canana

That's great to hear! I can't wait to see those!
Fri Dec 24, 2021 12:48 am CET

Alexandre Canana

Technically the Hatano is one equal-area fusion, at least one site says that it's composed of two custom projections joined at the equator
Fri Dec 24, 2021 12:50 am CET

Alexandre Canana

Basically, like the Strebe 2011, asymmetry and fusion at the same time.
Fri Dec 24, 2021 7:28 pm CET

Tobias Jung

Regarding the Hatano projection: The Geocart projection list says it’s a “modification of the Mollweide and Putnins P2' projections”.
https://www.mapthematics.com/P…

Putnins P2' is identical to Wagner IV, and Wagner IV is derived by “Umbeziffern” from Mollweide. Thus, it should be able to create Hatano by applying different configuration parameters to the northern and southern hemispheres on a customizable Wagner IV, just like the asymmetrical Wagner VII.b that I introduced recently was created using the customizable Wagner VII.

Regrettably, there’s (as far as I know) currently no map projection software which offers a customizable Wagner IV…
Sat Dec 25, 2021 2:22 pm CET

Alexandre Canana

Is it possible to apply the umbeziffern on, for example, a cylindrical projection?
Sun Dec 26, 2021 12:05 am CET

Alexandre Canana

or any other class besides the azimuthal ones or the pseudocylindrical ones?
Sun Dec 26, 2021 12:07 am CET

Tobias Jung

Yes, that’s possible. I’ve already applied Umbeziffern on Bottomley (conic), see
https://mapthematics.com/forum…
The result doesn’t look too bad but I think it doesn’t have much advantages compared to existing pseudocylindrical or lenticular projections.
This is an umbezifferte Gringorten (“miscellaneous” class) – just a proof of concept here (i.e. I didn’t even try to find an advantageous configuration):
https://map-projections.net/de…

And yes, it’s technical possible for cylindricals as well, but in this case, you can only modify the aspect ratio and the amount of areal inflation (and you can only INcrease the inflation of the parent projection, not DEcrease is) so there’s probably not much of a point to try this.
Sun Dec 26, 2021 2:32 pm CET

Alexandre Canana

Yeah, cylindricals have too much distortion in polar regions, especially two extremes which are the Lambert cylindrical equal area and the Mercator. Greenland is either the right size but flattened like a pancake or has a (more or less?) correct shape but is just huge.
Sun Dec 26, 2021 3:38 pm CET

Alexandre Canana

Yeah, cylindricals have too much distortion in polar regions, especially two extremes which are the Lambert cylindrical equal area and the Mercator. Greenland is either the right size but flattened like a pancake or has a (more or less?) correct shape but is just huge.
Sun Dec 26, 2021 3:38 pm CET

Alexandre Canana

BTW, do you know what happened to Mr Furuti's site? Or if it'll come back someday?
Sun Dec 26, 2021 6:52 pm CET

Alexandre Canana

It was of the most informative sites on the topic.
Sun Dec 26, 2021 7:06 pm CET

Tobias Jung

Regrettably, I don’t know what happened to the site, which indeed was absolutely great.
Since it’s gone for a few years now, I don’t think it’ll return. :-(
Sun Dec 26, 2021 7:22 pm CET

Alexandre Canana

That's quite a shame. :-(
Sun Dec 26, 2021 11:50 pm CET

Alexandre Canana

It's an honor to discuss map projections stuff with someone who's even so famous on the internet and as much as a map projection nerd as I am!
Sun Dec 26, 2021 11:53 pm CET

Alexandre Canana

If not more!
Sun Dec 26, 2021 11:58 pm CET

Tobias Jung

I’m not sure if I’m really that famous on the internet…
but – thank you nonetheless! :-)
Mon Dec 27, 2021 4:11 am CET

Alexandre Canana

Well, there's a paper on your site.
Mon Dec 27, 2021 2:24 pm CET

Alexandre Canana

«On» meaning about.
Mon Dec 27, 2021 3:51 pm CET

Alexandre Canana

You classify the Erdi-Krauz as Miscellanous but isn't it Pseudocylindrical?
Mon Dec 27, 2021 5:20 pm CET

Alexandre Canana

Correct me if I'm wrong.
Mon Dec 27, 2021 5:41 pm CET

Tobias Jung

Yes, Erdi-Krauz is a pseudocylindrical.
I can’t remember why I filed it as Miscellanous – maybe it was simply a mistake. Thanks for pointing that out, I just corrected it.
Mon Dec 27, 2021 5:53 pm CET

Alexandre Canana

You're welcome, Mr Jung.
Mon Dec 27, 2021 8:51 pm CET

Alexandre Canana

What projection would you recommend for a wall map for a bedroom?
Mon Dec 27, 2021 8:52 pm CET

Tobias Jung

I can’t recommend a specific projection here, because that depends on a lot of things… Is this supposed to be a purely decorative map, or do you want to obtain information from it? Is it more important to you to keep the sizes or the shapes? Are you free to select any aspect ratio, or are there any limits (because of the available space)? etc.
And even if those questions are answered, there is probably still a bunch of projections that’ll do the job…
Mon Dec 27, 2021 9:26 pm CET

Alexandre Canana

I just want a balanced view of the world, so a compromise projection would be good
Mon Dec 27, 2021 9:56 pm CET

Alexandre Canana

Because I do want to obtain information from it but I don't either good shapes and wrong areas or bad shapes and good areas.
Mon Dec 27, 2021 9:59 pm CET

Alexandre Canana

I just can't decide on the compromise.
Mon Dec 27, 2021 10:02 pm CET

Tobias Jung

Well, Winkel Tripel (both original and Bartholomew) is always a good choice for compromise projections. Personally, I prefer Canters W09 or Frančula XIII … or my F13 Copycat *grin*…
Mon Dec 27, 2021 10:04 pm CET

Alexandre Canana

Thanks for the advice.
Mon Dec 27, 2021 10:14 pm CET

Alexandre Canana

I'm want to get John Snyder's Flattening the Earth but I haven't found it anywhere. I want to become a translator so I could read that book and then translate it to Portuguese.
Mon Dec 27, 2021 11:59 pm CET

Tobias Jung

A good book store should be able to order it, even it it’s not available in your country. Of course then it will take some time before it’s delivered.
ISBN-10: 0226767477
ISBN-13: 978-0226767475
Tue Dec 28, 2021 1:59 am CET

Alexandre Canana

Actually it isn't available in Portugal, I even went to 2 bookstores in Lisbon and they didn't have it.
Tue Dec 28, 2021 1:26 pm CET

Alexandre Canana

But I won't give up trying to adquire it.
Tue Dec 28, 2021 1:26 pm CET

Alexandre Canana

I have never given up before, and I won't start doing it now.
Tue Dec 28, 2021 1:37 pm CET

Alexandre Canana

I also plan to join mapthematics.com
Tue Dec 28, 2021 4:46 pm CET

Alexandre Canana

I'd love to discuss projections with Daan Strebe as well.
Tue Dec 28, 2021 5:52 pm CET

Alexandre Canana

He created a lot of interesting/fun/useful map projections!
Tue Dec 28, 2021 6:01 pm CET

Tobias Jung

Oh yes, please do join the forum! It’s a bit quiet over there, so every new member is, in my opinion, most welcome!
Tue Dec 28, 2021 6:39 pm CET

Alexandre Canana

How do I get register there?
Tue Dec 28, 2021 6:43 pm CET

Alexandre Canana

I'm extremely happy to announce I'm now, as from today, a member of the forum!
Wed Dec 29, 2021 2:41 pm CET

Alexandre Canana

Which Canters projection do you like the best?
Tue Jan 25, 2022 10:44 pm CET

Tobias Jung

I can’t name just one favourite.
W14 used to be my favorite for a long time, but meanwhile I like the W13 and the Wagner IX optimization (W09) just as much. W11 has, despite its “wacky” shape, a great representation of the continents. Same goes for W30 (considering it’s an equal-area projection).
Thu Jan 27, 2022 8:17 am CET

Alexandre Canana

What kind of representation of the poles do you prefer on a map projection? Normal aspect pole or meta-pole? Pole as a point or singular pole?(line,circular arc, circle,semiellipse, curved line,etc)?
Thu Jan 27, 2022 10:34 am CET

Tobias Jung

All of this has its place, but purely aesthetically speaking, I’m definitely a friend of normal-aspect poles and curved pole lines or (as you might guess) pointed poles that at first glance look like pole lines.
Thu Jan 27, 2022 10:47 am CET

Alexandre Canana

Yeah, as long as I know that Earth's poles are points I don't need to always use a pointed-polar projection.
Thu Jan 27, 2022 1:56 pm CET

Alexandre Canana

As long as I don't use the Cylindrical Equal Area that is.
Thu Jan 27, 2022 1:58 pm CET

Alexandre Canana

I think it's problem is the the length of the pole line and the map frame which detracts a lot from the Globe.
Thu Jan 27, 2022 4:11 pm CET

Alexandre Canana

Two reasons for it having such squashed/flattened shapes-
Thu Jan 27, 2022 4:13 pm CET

Alexandre Canana

So when in the 20th century most Pseudocylindrical are developed, the authors chose ratios like half the length or one-third the length of the equator.
Fri Jan 28, 2022 11:28 am CET

Alexandre Canana

Mr Jung, are you going to add the 7 Baranyi projections?
Sat May 28, 2022 4:06 pm CEST

Alexandre Canana

I'm asking this because they were developed the same way as Dr. Arthur Robinson's design, instead of using mathematical formulae, a trial and error approach using interpolation.
Sat May 28, 2022 4:10 pm CEST

Tobias Jung

I will add Baranyi I, II, III and IV sometime (hopefully) soon.
Regrettably, I don’t have a map projection software that can render V, VI and VII.
Sat May 28, 2022 5:40 pm CEST

Alexandre Canana

Sadly, G.Projector only has the his 4th projection
Sun May 29, 2022 12:10 pm CEST

Tobias Jung

No, in the latest update, Baranyi I to III were added. :-)
Sun May 29, 2022 1:28 pm CEST

Alexandre Canana

Oh, really? That's really great!
Sun May 29, 2022 7:05 pm CEST

Alexandre Canana

«Using Zelenka's method» I guess, like with the Robinson, the Baranyi pseudocylindricals's interpolation method wasn't explicitly specified?
Sun May 29, 2022 7:07 pm CEST

Tobias Jung

Probably, but I don’t know.
Sun May 29, 2022 8:05 pm CEST

Alexandre Canana

Which one of the Baranyi projections do you like the most?
Mon May 30, 2022 5:27 pm CEST

Alexandre Canana

Also, what is your opinion about each Baranyi projection?
Thu June 02, 2022 1:06 am CEST

Tobias Jung

I have to admit that I never inspected the Baranyi projections well enough to form a sensible judgement.
For example, I always thought they’d be pseudocylindricals – because Mr. Anderson listed them as such
http://spatial.ucsb.edu/archiv…
– but now I noticed that Baranyi III to VII do not have a constant scale along each parallel, so strictly speaking, they are not pseudocylindric.
Currently, my favorites are VII, III and IV (in that order, sorted descending). But sometimes I change my mind over time…
Thu June 02, 2022 2:01 pm CEST

Alexandre Canana

I'm going to translate D.H.Maling's "A review of some Russian map projections"
Fri July 08, 2022 12:19 am CEST

Alexandre Canana

I wonder if it's legal to publish my translation?
Fri July 08, 2022 9:35 pm CEST

Tobias Jung

I think it’s a great idea to translate good texts, BUT – I’m fairly certain it’s NOT legal to publish a translation without permission from the original author or his/her heirs (unless the author died long ago, as far as I know 70 years in many countries).
I am not a lawyer, but if you want to publish a translation, you really should consult one.
Fri July 08, 2022 11:14 pm CEST

Alexandre Canana

Well I still won't be publishing it because I'm still working on the translation on the first part of his paper
Sat July 09, 2022 12:33 am CEST

Alexandre Canana

Thank you for the advice though
Sat July 09, 2022 12:33 am CEST

Alexandre Canana

I'm translating it to my native Language BTW
Sat July 09, 2022 12:40 am CEST

Tobias Jung

“I'm translating it to my native Language BTW”
Yes, I thought so, because… well, if I’d translate anything, it would be either FROM my native language to English (e.g. Wagner’s text or Frančula’s 1971 paper) or TO my native language. So I just assumed you’d do the same… :-)
Sat July 09, 2022 3:33 am CEST

Alexandre Canana

In my case it's Portuguese( European)
Sat July 09, 2022 4:50 pm CEST

Alexandre Canana

Why was it that b4 we couldn't send any new comments?
Mon July 11, 2022 12:41 am CEST

Tobias Jung

I had to fix something in the part of the scripts that fights off comment spam, but sometimes I didn’t feel like it, sometimes I didn’t have the time. So I just turned off the comment function for a while.
Mon July 11, 2022 1:53 am CEST

Alexandre Canana

I see.
Mon July 11, 2022 10:46 am CEST

Alexandre Canana

Mr Jung, are you going to add the other Azimutal Projections?
Tue Aug 02, 2022 12:47 pm CEST

Tobias Jung

It depends:
Of course I need a software that can render them, and usually I only add projections that are useful (in one way or another) for world maps, although there already may be a few exceptions…

Which azimuthal projections specifically do you feel are missing?
Tue Aug 02, 2022 12:55 pm CEST

Alexandre Canana

The 3 Russian modifications, Urmayev I and II and Ginzburg I and II
Wed Aug 03, 2022 3:12 pm CEST

Alexandre Canana

And the Orthographic and Gnomonic projections
Wed Aug 03, 2022 3:13 pm CEST

Alexandre Canana

Urmayev I and II and Ginzburg I and II were made from the Azimuthal Equal Area like the Miller Cylindrical was made from the Mercator, by adding a second term into the equations of the original/parent projection, reducing in the case of Ginzburg and Urmayev the angular deformation of the Lambert Azimuthal at the cost of losing equivalence, just like how the Miller reduces the Mercator's areal deformation at the cost of losing conformality.
Wed Aug 03, 2022 3:19 pm CEST

Tobias Jung

Urmayev I and II: Can’t add them, no support by the applications I’m using.
Ginzburg I and II: Yes, I guess I will add them at some point.
Gnomonic projection: Probably not because it’s really not suited for world maps (or even hemispheric maps).
Orthographic projection: Hmmm. It only shows less than a hemisphere, in my opinion, there’s too much missing for useful comparisons.
Wed Aug 03, 2022 11:12 pm CEST

Alexandre Canana

Thank you for the info!
Thu Aug 04, 2022 12:03 am CEST

Alexandre Canana

Keep up the good work!
Thu Aug 04, 2022 12:03 am CEST

Alexandre Canana

Which rearrangement do you like the best? The one by Constant Xarax or the one by Luca Concialdi?
Wed Aug 31, 2022 7:33 pm CEST

Alexandre Canana

Are you going the add the other Baranyi Projections?
Sun Nov 27, 2022 12:51 am CET

Tobias Jung

Yes, I will, but I don't know if I’ll get around to it this year.
Sun Nov 27, 2022 4:00 am CET

Alexandre Canana

Okay, thank you very much for the information.
Sun Nov 27, 2022 11:55 am CET

Alexandre Canana

Merry Christmas!
Sat Dec 24, 2022 5:31 pm CET
characters remaining: 2048
  
X Icon

Please leave the following four input field blank in any case!