My Projection Collection:
Compare Projections
Patterson Cylindrical vs. Equirectangular (35.6°)
| Patterson Cylindrical | Equirectangular (35.6°) | |
|---|---|---|
| Creator | Tom Patterson, Bojan Savric, Bernhard Jenny (2014) | Marinus of Tyre (about AD 100) |
| Group | Cylindric | Cylindric |
| Property | Compromise | Equidistant |
| Other Names | — | — |
| Remarks | The Patterson cylindrical balances polar exaggeration against maintaining the familiar shape of continents. Read Introducing the Patterson Cylindrical Projection on cartographicperspectives.org. Here on map-projections.net there’s an article about Patterson Cylindrical. Note: Up to the end of 2019 I showed a wrong rendition of the Patterson projection here (having a false aspect ratio). The current image is correct. Read the blogpost about this. |
Here: Standard parallels at 35.6° (= 35° 36′) North/South. Values around these standard parallels nicely fill the space of a ISO-219 series A (A3, A4 etc.) paper sheet while at the same time leaving enough space for a legend above or below the map. |
| recommended comparisons | Miller Equirectangular (28°) Equirectangular (35.6°) |
Gall Isographic Patterson |
|
This pairing is among the list of recommended pairings – but why? To clearly show how the Patterson projection »balances polar exaggeration against maintaining the familiar shape of continents«. |
||
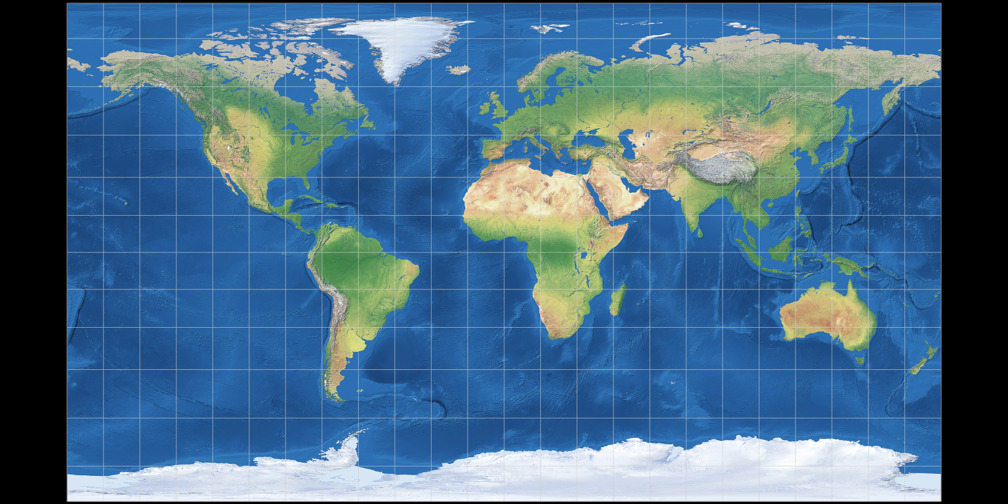
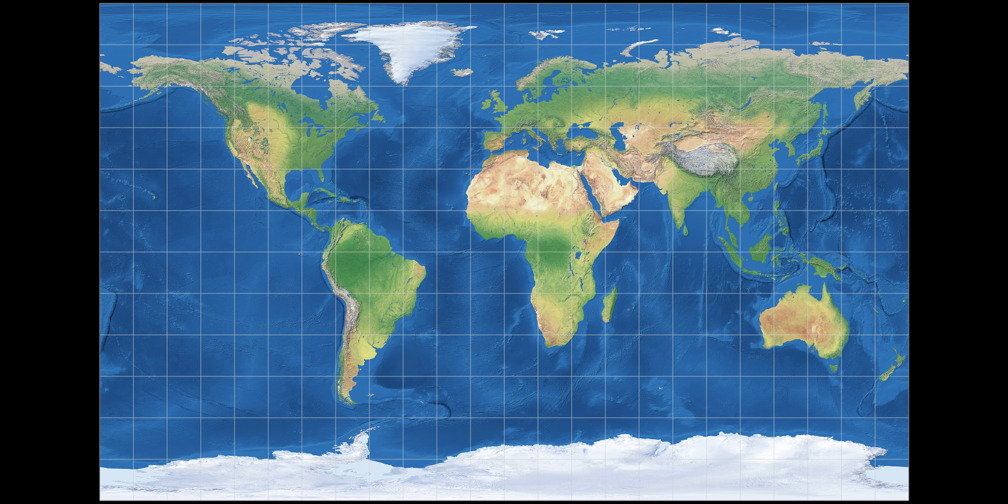
1. Comparison: Physical Map
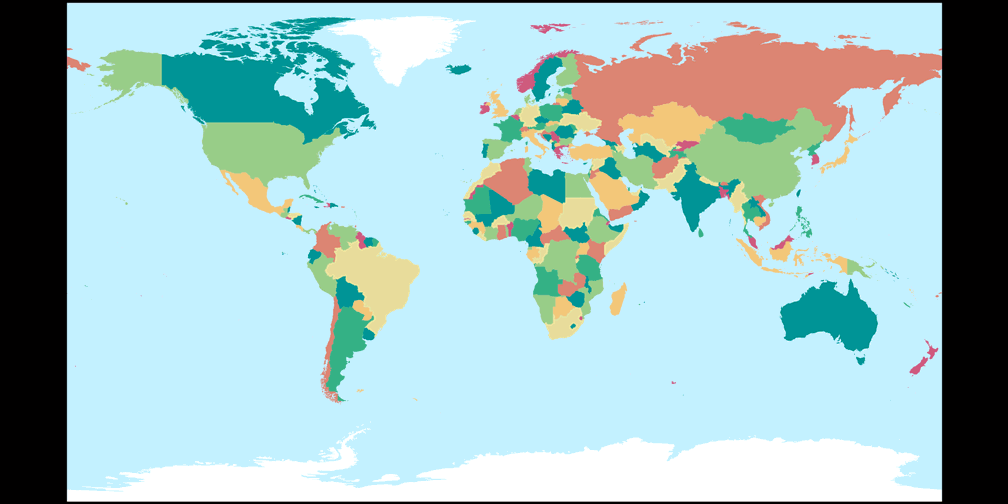
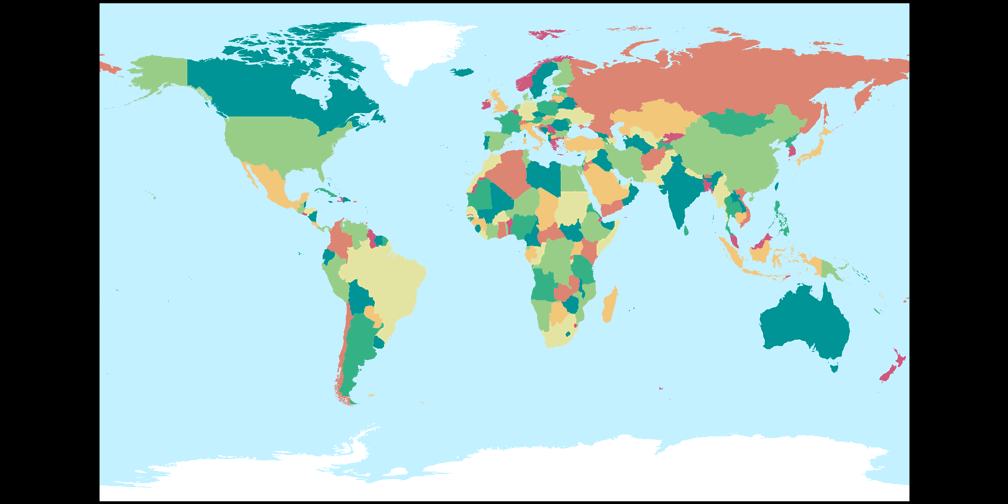
2. Comparison: Political Map
Patterson Cylindrical
Equirectangular (35.6°)
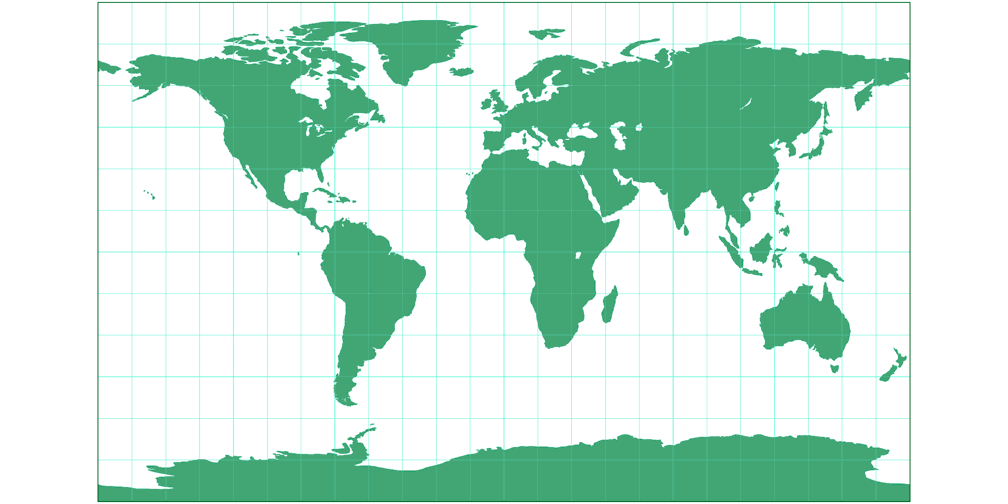
3. Comparison: Silhouette Map
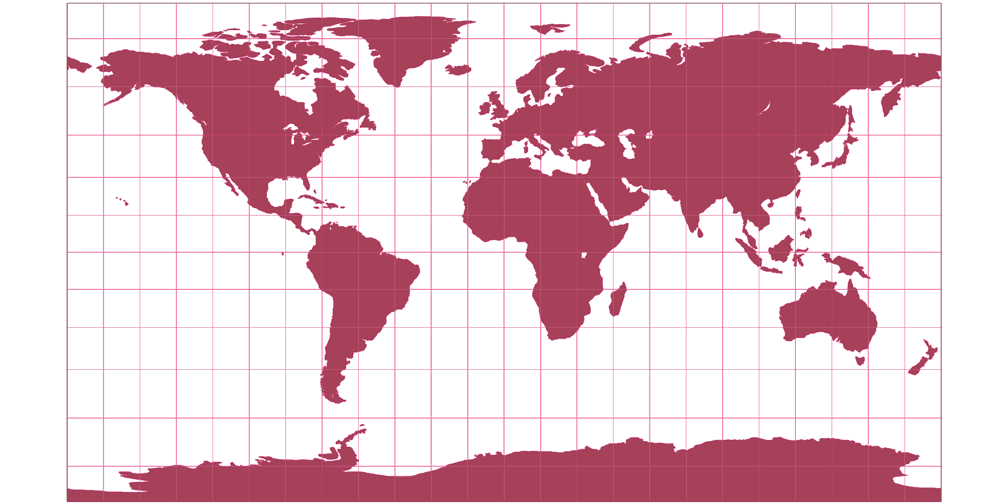
Patterson Cylindrical Silhouette Map c Tobias Jung
Equirectangular (35.6°) Silhouette Map c Tobias Jung
4. Comparison: Tissot Indicatrix, 30°
Patterson Cylindrical
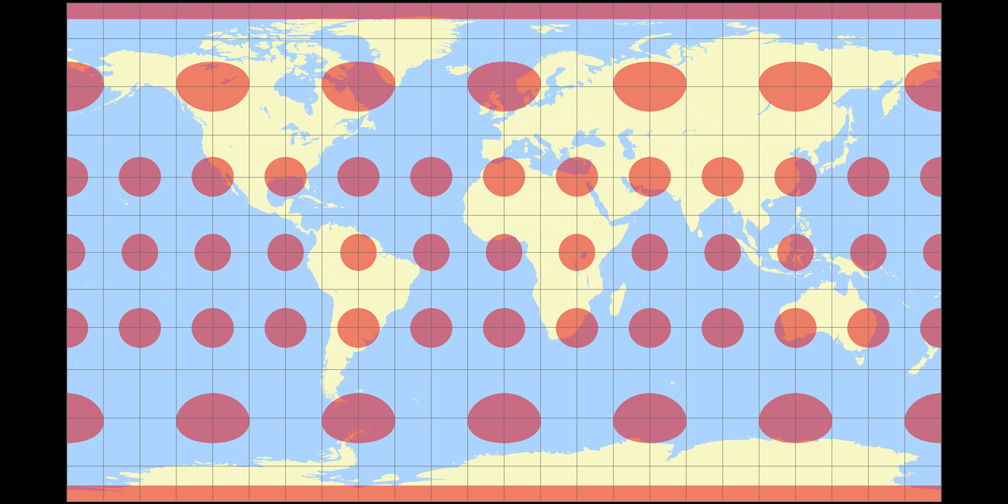
Equirectangular (35.6°)
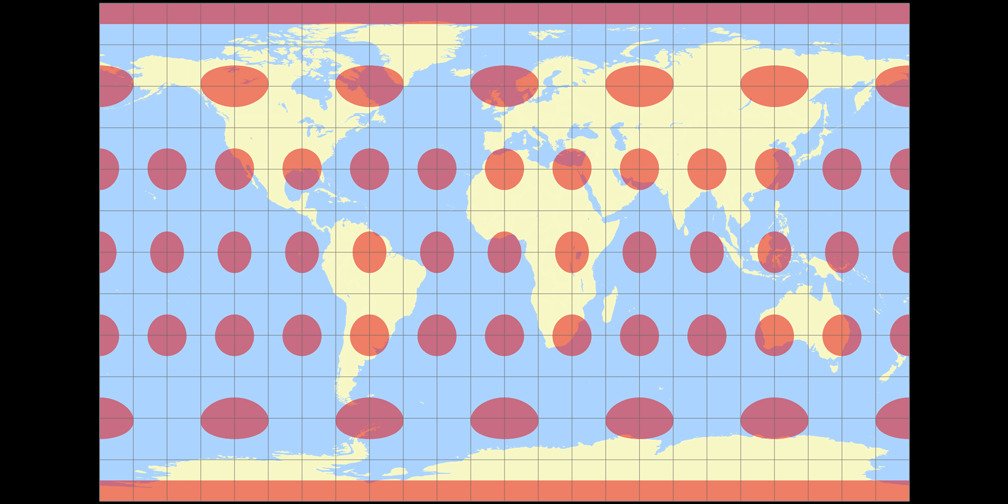
Patterson Cylindrical Tissot Indicatrix c Tobias Jung
Equirectangular (35.6°) Tissot Indicatrix c Tobias Jung