Compare Map Projections

[info]    Viewing options: South up    Flat oceans    Apply

The Wagner Projections (Part 1)

Karlheinz Wagner’s nine projections aren’t new – they were developed between 1932 and 1949 – and should be well-known to anybody who is interested in map projection. In past, they have been used in various atlases. However, in recent years they seem to slide into obscurity and they really don’t deserve that.

Since I really like Wagner’s work, and since the nine projections are rarely shown altogether – except for Dr. Böhm’s splendid (german) article Wagners Weltkartennetze –, I’d like to present them here.

There’s a lot to talk about nine different projections, so I decided to split up the article into parts.
Part 2 covers some examples of usage, part 3 takes a closer look at Wagner’s transformation method called Umbeziffern, part 4 present Wagner’s variations of Wagner VII, obtained by Umbeziffern, and the pending part 5 will cover Wagner variations by Canters and Böhm.
 

• Preface
• Wagner I - III
• Wagner IV - VI
• Wagner VII - IX
• Interim Conclusion
• References

Introduction

Wagner didn’t create projection that were completely new – instead, he used a process called Umbeziffern von Kartennetzen (»re-numbering of carthographic grids«, sometimes referred to as The Wagner transformation), which allowed him to apply pole lines to projections that show the pole as a point, and then to furtherly modify them.

Sounds too abstract?
OK, let’s have a closer look:

• Wagner I, II und III are, by Umbeziffern, derived from the Sinusoidal projection;
• Wagner IV, V and VI are derived from the Mollweide projection;
• Wagner VII, VIII and IX are descendants of (modified) equatorial azimuthal projections.

So these are the ancestors of the Wagner projection – but what about that »furtherly modify« I mentioned above?

• Wagner I, IV und VII are equivalent, just like their ancestors (so, they weren’t furtherly modified after the Umbeziffern);
• Wagner II, V and VIII introduce a (moderate) areal distortion in order to enhance the rendering of shapes (or, more scientific, in order to reduce angular distortion);
• and Wagner III, VI as well as IX totally refrain from equivalence in order to offer equally spaced parallels.

 

Here’s that lineup again, using a neatly arranged table:

Derived from	Equal-Area	Compromise	Equally Spaced Parallels
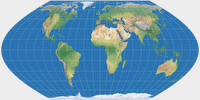
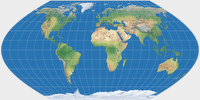
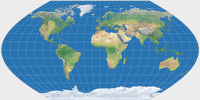
Sinusoidal Projection	Wagner I	Wagner II	Wagner III
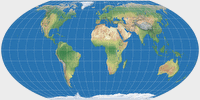
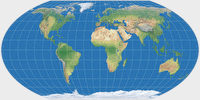
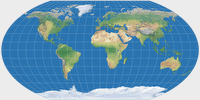
Mollweide	Wagner IV	Wagner V	Wagner VI
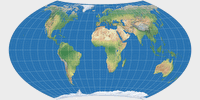
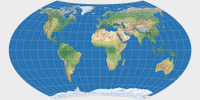
Equatorial Azimuthal projections	Wagner VII	Wagner VIII	Wagner IX

 

Before we examine the Wagner projection individually, I’d like to add two remarks:

– The ordinal numbers don’t refer to the chronological order of creation but to the order in which Wagner introduces them in this textbook Kartographische Netzentwürfe ^[1].
The numbering was initially used by J.P. Snyder ^[2], Wagner himself didn’t used this labels.

– For the projections II, V and VIII Wagner used the term vorgeschriebene Flächenverzerrung – prescribed area distortion – which to refers to the self-imposed limit that the areal enlargement between 60° north and south should not exceed 20%. Within this range you include most of the inhabited area of the earth without exaggerated areal distortion.

 

Wagner I, II and III – The Sinusoidal Descendants

Wagner I   (equal-area)

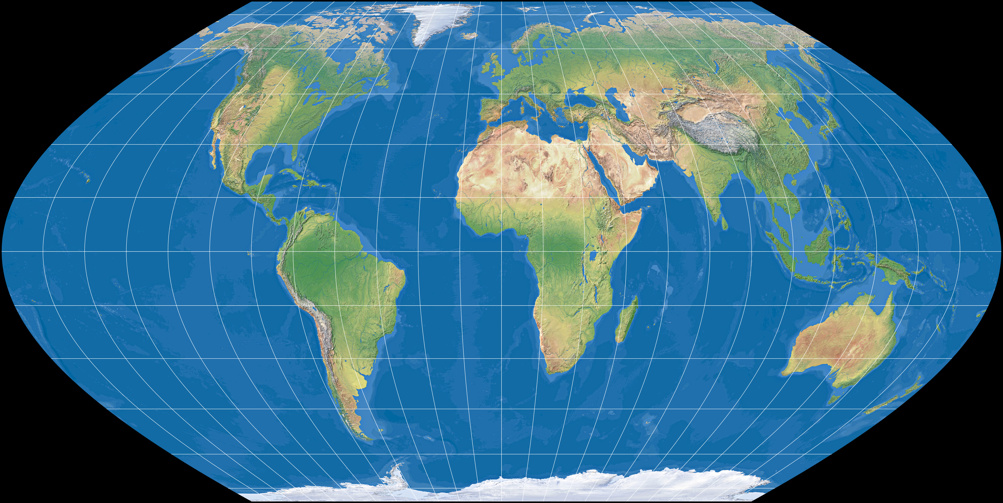
Wagner II   (moderate areal distortion)

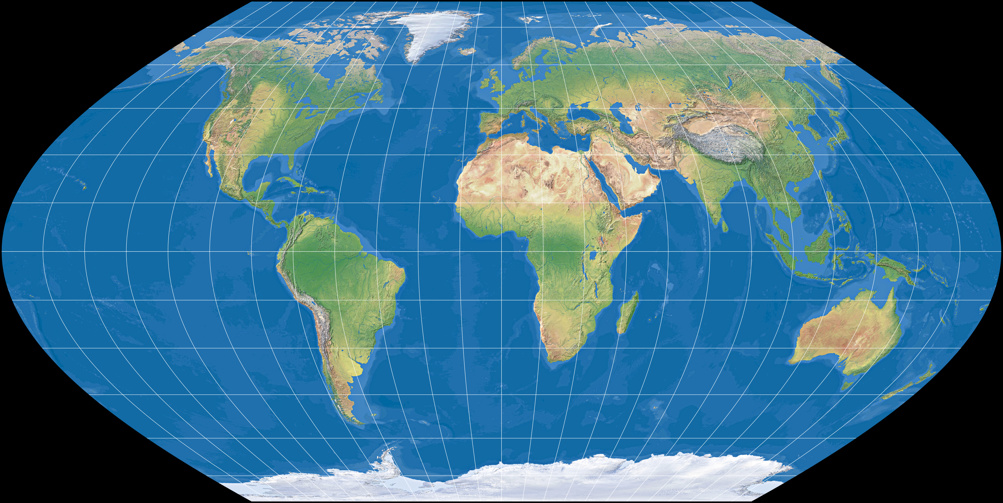
Wagner III   (equally spaced parallels)

You can easily see that projections II and III gradually move away from equivalence (which is maintained in the first projection) while gradually improving the shapes.
However, experts will notice that Wagner I is almost identical to Eckert VI, which was developed nearly 30 years earlier, while Wagner III has a striking resemblance with Eckert V:
Eckert VI vs. Wagner I  –  Eckert V vs. Wagner III

Wagner specifically points out this resemblance in his textbook Karthographische Netzentwürfe. So why did he even bother to create this projection?
Simply put, Wagners formulæ are easier to handle than Eckert’s. Remember that back in those days, there weren’t any computers or other electronic calculators, so simplifying a mathematical formula really did matter.

Except from equally spaced parallels, the Wagner III has another metric property: It is equidistant on the equator and the central meridian. Wagner proposed that you can choose a different parallel to be equidistant (without changing the central meridian’s property) in order to achieve »a better distribution of distortions«. An according image, equidistant on 40° North/South is available on this website.

Regarding the appearances: Don’t these projections look kinda… strange?
Nowadays, sinusoidal meridians are rarely to be seen, almost all common non-cylindric projections have elliptic meridian curves (we’ll come back to them in a moment) for the simple reason that elliptic projections usually have lower angular distortions.

While Wagner’s (and Eckert’s) projections with sinusoidal curves do have their advantages over the elliptic curves projections in certain areas (e.g. near the poles) – at the end of the day, I guess I’d always choose the latter. Unless you want to favor an unusual design which sometimes might serve as a nice eye-catcher. Apart from that, there is one situation in which the sinusoidal variant might actually be the better choice – I’ll come back to this later (in the pending part 2 of this article).

But now, let’s head on to Wagner projections with elliptic curves…

 

Wagner IV, V and VI – The Mollweide Descendants

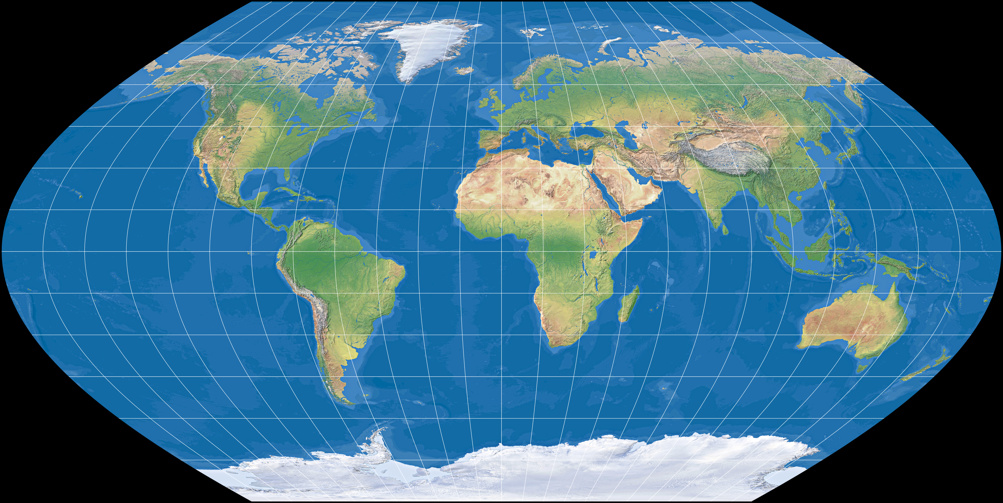
Wagner IV   (equal-area)

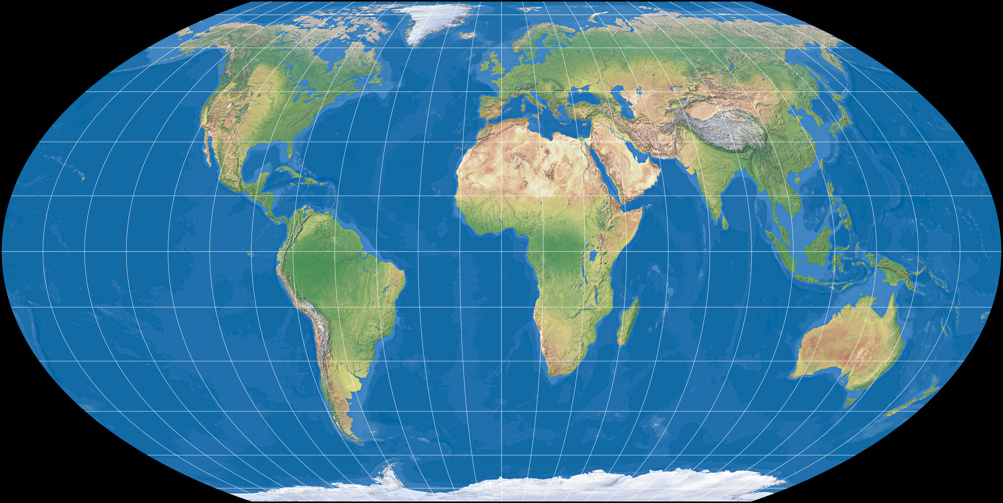
Wagner V   (moderate areal distortion)

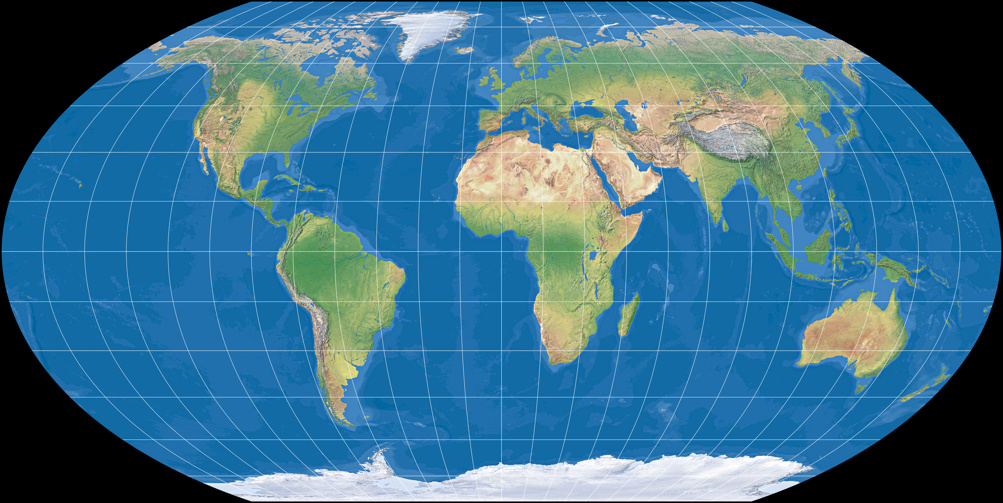
Wagner VI   (equally spaced parallels)

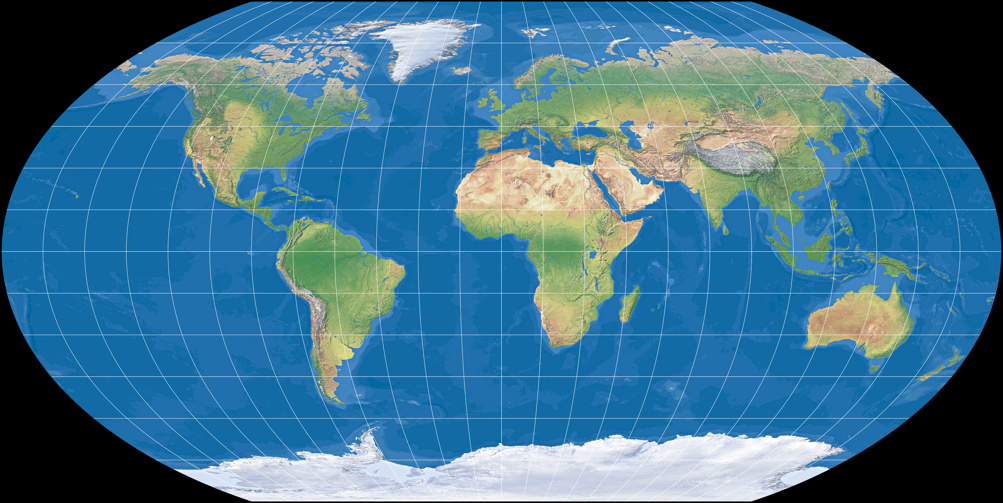
It’s the same transformation – going from equal-area to equally spaced parallels – as on the first sequence.
And again, there’s some similarity to Eckert’s projections but not nearly as close as before:
Wagner IV vs. Eckert IV  –  Wagner VI vs. Eckert III

It’s obvious that Wagner’s projections show a more pronounced curvature – and of course, they have edged pole line corners as opposed to the curved corners on Eckert’s. And although the Eckert projections have slightly better distortion values, I prefer the Wagner projections: I just like the curvature, the corners – and the less incisive arctic stretching. Admittedly, Australia’s shape is better on Eckert’s versions…

Let’s go into detail about the three projections of this sequence:
The usefulness of equivalent projections is, I think, not up for debate; and both Wagner IV as well as Eckert IV are outstanding specimen of that kind. So whether the Wagner or the Eckert variant is to be preferred, is purely a matter of taste.
(By the way: I didn’t need it, but just for the fun of it I generated a Wagner IV approximation that can be used in Flex Projector. Read more about it in the Approximations chapter.)

Wagner V is a great compromise projection when you need a pseudocylindric projection that doesn’t move too far away from equivalence. There’s no match for that on Eckert’s projections, but the application Geocart offers a own mixture of Eckert III and IV; or you can you Flex Projector’s »Simple Mixer« to build your own – so you’ll can get an Eckert counterpart to Wagner V after all.

Eckert III and Eckert IV mixed (left) compared to Wagner V (right)

As I’ve said before, Wagner VI has equally spaced parallels – but what good are they?
Well, quite obviously, they result in comparatively low distortion of shapes, especially in higher latitudes – but at a price. Quoting Wagner:

Die Zunahme der Flächenvergrößerung ist doch schon recht erheblich.

The areal enlargement is quite considerable.

Wagner apparently preferred the projections with »prescribed area distortion« – and he repeatedly points out that you might calculate them with different parameters then he chose for the projections he introduced. Again, please refer to the upcoming second part of this article, where I’ll cover this matter while also showing useful usages for equally spaced parallels.

Now, let’s head over to the in my opinion most interesting sequence of Wagner projections.

 

Wagner Wagner VII, VIII and IX – The Azimuthal Descendants

Wagner VII   (equal-area)

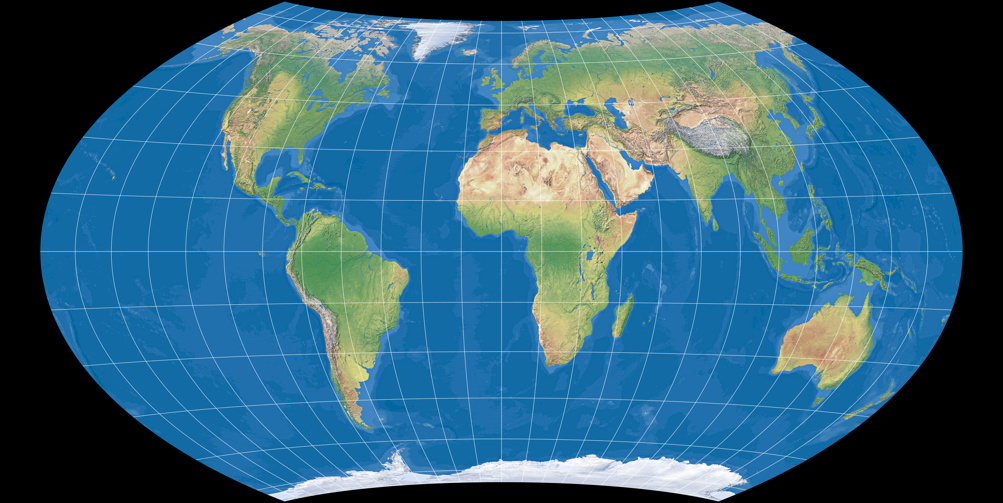
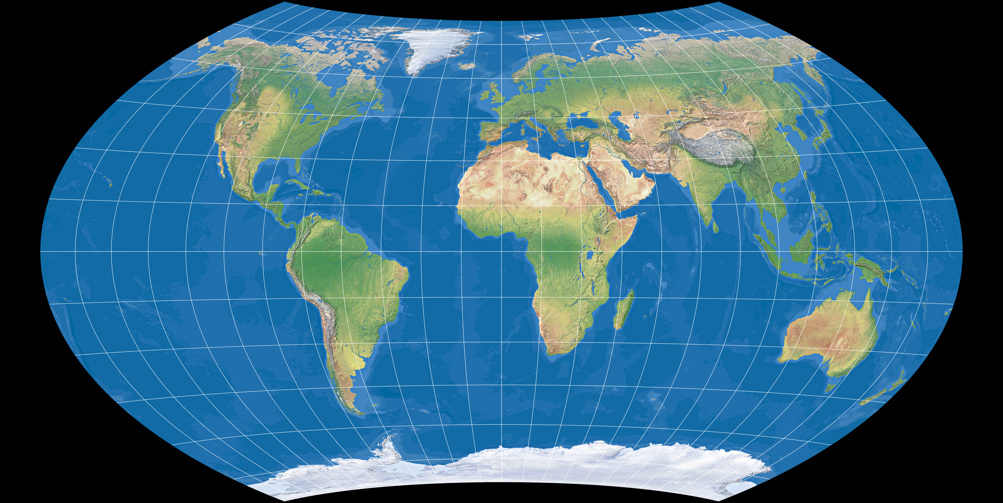
Wagner VIII   (moderate areal distortion)

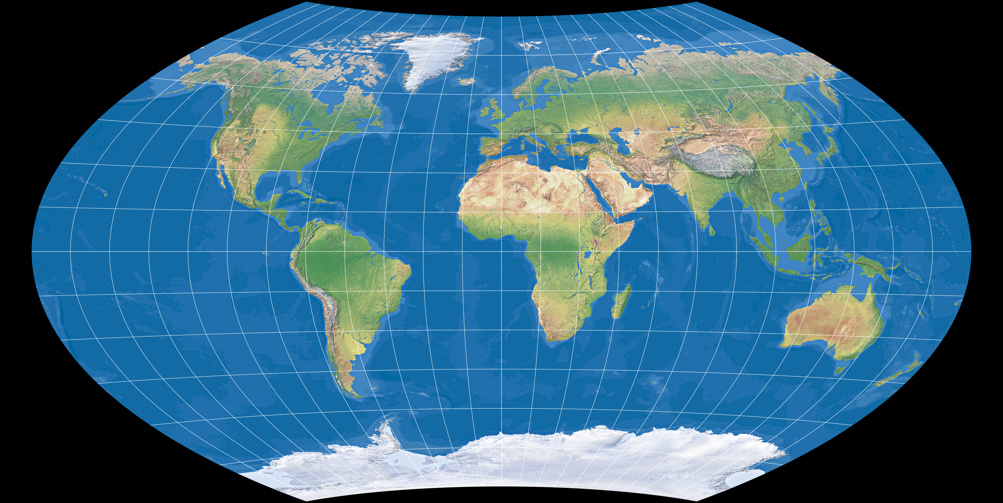
Wagner IX   (equally spaced parallels)

Wagner VII is a derivation of the Hammer projection which was equipped with a pole line. And since the Hammer on his part is a derivation of the equatorial equal-area azimuthal projection, Wagner VII is equivalent, too. The curved parallels reduce angular deformation out toward the edges and thus, we get a very beautiful projection – one of my two favorite equal-area projections! (The other favorite being the Strebe 1995.)

Wagner VIII is the counterpart to Wagner II resp. Wagner V: Again, Wagner derives a projection with prescribed area distortion from the equal-area model.
Although it has been pointed out to me that the improvements to Africa and South America are minor (…) If you’re going to depart from equivalence, be bold, I say ^[4] … I really like the Wagner VIII! In my eyes, the improvements aren’t that minor after all. The vertical stretching of Africa (and Australia, for that matter) is pleasantly reduced:
Wagner VII vs. Wagner VIII

Although I do have to admit: The differences leap to the eye in direct comparison only. When I was looking at a world map in an atlas some time ago, it indeed took a while for me to determine whether it was the Wagner VII oder VIII…

Still, I stick to my opinion that the Wagner VIII is a highly recommendable projection for general-use maps, e.g. wallpaper maps or world maps in school atlases – unless absolute equivalence is mandatory. In that case, Wagner VII is a magnificent option which preserves area measure without too much distortion of shapes.

And finally, we get to the variant with curved, equally spaced parallels. Of course, because of their non-concentric curvature, they are equally spaced along the central meridian only. The Wagner IX therefore introduces an areal enlargement that is more or less comparable to the enlargement of Wagner III and VI – but oddly enough, I think it doesn’t seem that bad here.
Maybe that’s because of the curved parallels which result in Greenland, for example, being stretched horizontally a bit less…

Therefore, I can say: Cautiously used, the Wagner IX might be a good choice for general-use world maps, too.
Maybe using a small modification:

Again, Wagner points out that compressing the projection horizontally results in »a better distribution of distortions«. As an example, he adds a figure in which the horizontal values were multiplied by 0.88. He chose that specific value in order to achieve an outer shape which approaches the Winkel Tripel (which at that time, already seemed to be quite popular in Germany).
Personally, I think that compression is a bit too much. But hey, Wagner used it as an example only. So, you might find out for yourself if, maybe, a factor of 0.92 or something might suit you better.

 

Interim Conclusion

Wagner presented a family of world map projection that is almost universally usable. Offering a selection of sinusoidal and elliptic meridians, straight and curved parallels, with three different metric properties each, gradually moving from equal-area to equally spaced parallels nearly all possible applications for world maps are covered (as long as you talk about uninterrupted flat-pole projections, of course).

In The Wagner Projections (Part 2): Usage I’d like to support that claim by showing a few examples.

 

References

1. ↑ Wagner, Karlheinz:
   Kartographische Netzentwürfe.
   Leipzig 1949.
2. ↑ Snyder, John P.:
   Flattening the Earth: Two Thousand Years of Map Projections.
   Chicago 1993.
3. ↑ Capek, Richard 2001:
   Which is the Best Projection for the World Map?
   icaci.org/files/documents/ICC_proceedings/ICC2001/icc2001/file/f24014.pdf
4. ↑ see Distortion Value Tables in Flex Projector
5. ↑ posted by daan Strebe during a discussion in the mapthematics.com forum

 

Back to Selected Projections  •  The Wagner Projections (Part 2)  •  Go to top